《2026年天利38套中考试题精选数学浙江专版》

23. (本小题满分10分)已知二次函数$y=ax^{2}+bx+3$($a$,$b$为常数且$a\neq0$)的图象经过点$(-1,0)$,对称轴为$x=1$.
(1)求二次函数的表达式.
(2)函数图象上有两个点$A(x_{1},y_{1})$,$B(x_{2},y_{2})$.
①当$-1\leq x_{1}\leq0$,$\frac{1}{2}\leq x_{2}\leq\frac{3}{2}$时,求$y_{1}-y_{2}$的最大值.
②若$m\leq x_{1}\leq m+1$,$m+2\leq x_{2}\leq m+3$时,存在$y_{1}-y_{2}=1$,求$m$的取值范围.

答案： 23.二次函数的图象与性质
解：
(1)解法一（一般法）：
∵二次函数$y = ax^{2} + bx + 3$（$a$，$b$为常数且$a \neq 0$）的图象经过点$(-1, 0)$，对称轴为$x = 1$，
∴$\begin{cases} -\frac{b}{2a} = 1, \\ a - b + 3 = 0 \end{cases}$ 解得$\begin{cases} a = -1, \\ b = 2 \end{cases}$
∴$y = -x^{2} + 2x + 3$.（4分）
解法二（交点法）：
∵二次函数$y = ax^{2} + bx + 3$（$a$，$b$为常数且$a \neq 0$）的图象经过点$(-1, 0)$，对称轴为$x = 1$，
∴二次函数的图象与$x$轴的另一个交点为$(3, 0)$，且该函数图象与$y$轴的交点坐标为$(0, 3)$.
∴设二次函数表达式为$y = a(x + 1)(x - 3)$，
将点$(0, 3)$的坐标代入得$a = -1$.
∴$y = -(x + 1)(x - 3) = -x^{2} + 2x + 3$.（4分）
(2)①[第1步，根据二次函数的性质，确定函数的单调性]
$y = -x^{2} + 2x + 3 = -(x - 1)^{2} + 4$.
∵$a = -1 ＜ 0$，
∴抛物线开口向下.
当$x ＜ 1$时，$y$随着$x$的增大而增大，
当$x ＞ 1$时，$y$随着$x$的增大而减小.（5分）
[第2步，根据单调性得出$y_{1}$的最大值和$y_{2}$的最小值]
∴当$-1 \leq x_{1} \leq 0$时，在$x = 0$处，$y_{1}$取得最大值$3$.
当$\frac{1}{2} \leq x_{2} \leq \frac{3}{2}$时，在$x = \frac{1}{2}$和$x = \frac{3}{2}$处，$y_{2}$均取得最小值为$y_{2} = -(\frac{1}{2})^{2} + 2×\frac{1}{2} + 3 = \frac{15}{4}$.（6分）
[第3步，求出$y_{1} - y_{2}$的最大值]
∴$y_{1} - y_{2}$的最大值为$3 - \frac{15}{4} = -\frac{3}{4}$.（7分）
②[第1步，求出两个已知取值范围的端点值]
当$x_{1} = m$时，$y_{1} = -m^{2} + 2m + 3$；
当$x_{1} = m + 1$时，$y_{1} = -m^{2} + 4$；
当$x_{2} = m + 2$时，$y_{2} = -m^{2} - 2m + 3$；
当$x_{2} = m + 3$时，$y_{2} = -m^{2} - 4m$.
[第2步，列出满足题意的不等式组，并解不等式组得出答案]
∵存在$y_{1} - y_{2} = 1$，
当$m + 1 \leq 1$时，$-m^{2} + 2m + 3 \leq y_{1} \leq -m^{2} + 4$，$-m^{2} - 4m \leq y_{2} \leq -m^{2} - 2m + 3$，
则$\begin{cases} (-m^{2} + 2m + 3) - (-m^{2} - 2m + 3) \leq 1, \\ (-m^{2} + 4) - (-m^{2} - 4m) \geq 1 \end{cases}$
解得$-\frac{3}{4} \leq m \leq 0$.
当$m + 1 ＞ 1$，且$m ＜ 1$，即$0 ＜ m ＜ 1$时，$-m^{2} + 2m + 3 \leq y_{1} \leq 4$，$-m^{2} - 4m \leq y_{2} \leq -m^{2} - 2m + 3$，或$-m^{2} + 4 \leq y_{1} ＜ 4$，$-m^{2} - 4m ＜ y_{2} \leq -m^{2} - 2m + 3$，
则$\begin{cases} 0 ＜ m ＜ 1, \\ (-m^{2} + 2m + 3) - (-m^{2} - 2m + 3) ＜ 1, \\ 4 - (-m^{2} - 4m) \geq 1 \end{cases}$
或$\begin{cases} 0 ＜ m ＜ 1, \\ (-m^{2} + 4) - (-m^{2} - 2m + 3) ＜ 1, \\ 4 - (-m^{2} - 4m) \geq 1 \end{cases}$
解得$0 ＜ m \leq \frac{1}{4}$.
当$m \geq 1$时，$-m^{2} + 4 \leq y_{1} \leq -m^{2} + 2m + 3$，$-m^{2} - 4m \leq y_{2} \leq -m^{2} - 2m + 3$，
则$\begin{cases} m \geq 1, \\ (-m^{2} + 4) - (-m^{2} - 2m + 3) \leq 1, \\ (-m^{2} + 2m + 3) - (-m^{2} - 4m) \geq 1 \end{cases}$
无解.
综上，$-\frac{3}{4} \leq m \leq \frac{1}{4}$.（10分）

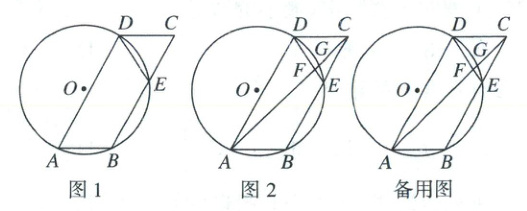
24. (本小题满分12分)如图1,在$□ ABCD$中,$\angle DAB=60^{\circ}$,过$A$,$B$,$D$三点的$\odot O$交$BC$于点$E$,连接$DE$.
(1)求证:$\triangle CDE$为等边三角形.
(2)如图2,连接$AC$,分别交$DE$和$\odot O$于点$F$,$G$,若$CE=2$,$BE=4$.
①求$AC$的长.
②求$\frac{FG}{DE}$的值.

答案：
24.圆的综合题+平行四边形的性质+等边三角形的判定与性质+圆内接四边形的性质+相似三角形的判定与性质+勾股定理
解：
(1)证明：
∵四边形$ABCD$是平行四边形，
∴$\angle C = \angle DAB = 60^{\circ}$.（2分）
∵四边形$ABED$是圆内接四边形，
∴$\angle DEC = \angle DAB = 60^{\circ}$.
∴$\triangle CDE$为等边三角形.（4分）
(2)①[第1步，作$CM \perp AB$，求出$\angle CBM$及$BC$]
过点$C$作$CM \perp AB$交$AB$的延长线于点$M$（巧作辅助线：构造直角三角形，利用勾股定理求线段），
　　　　　　　　　
由
(1)知$\triangle CDE$为等边三角形，
∴$CD = DE = CE = 2$.
在$□ ABCD$中，$\angle DAB = 60^{\circ}$，
∴$\angle ABC = 120^{\circ}$，$AB = CD = 2$.
∴$\angle CBM = 60^{\circ}$.
∵$CE = 2$，$BE = 4$，
∴$BC = 6$.（6分）
[第2步，利用特殊角的三角函数值求得$CM$，$BM$，进而得$AM$]
在$Rt \triangle CBM$中，$BM = BC · \cos 60^{\circ} = 3$，$CM = BC · \sin 60^{\circ} = 3\sqrt{3}$，
∴$AM = AB + BM = 5$.（7分）
[第3步，利用勾股定理求得结果]
∴在$Rt \triangle ACM$中，$AC = \sqrt{AM^{2} + CM^{2}} = 2\sqrt{13}$.（8分）
②[第1步，证明$\triangle FAD \sim \triangle FCE$，求得$AF$，$DF$，$EF$]
∵$AD // BC$，
∴$\triangle FAD \sim \triangle FCE$（难点：本题要求$FG$，需证明$\triangle FEG \sim \triangle FAD$，从而得到$FG · AF = FD · EF$，所以必须求得$AF$，$FD$，$EF$三条线段长度，由于$AC$，$DE$已知，便可利用$\triangle FAD \sim \triangle FCE$解决问题）.
∵$\frac{DF}{EF} = \frac{AF}{CF} = \frac{AD}{CE} = 3$.
∴$AF = \frac{3}{4}AC = \frac{3\sqrt{13}}{2}$，$DF = \frac{3}{4}DE = \frac{3}{2}$，$EF = \frac{1}{4}DE = \frac{1}{2}$.（10分）
[第2步，证明$\triangle FEG \sim \triangle FAD$，求$FG$]
连接$EG$.
∵$\overset{\frown}{DG} = \overset{\frown}{DG}$，
∴$\angle DEG = \angle DAF$.
又
∵$\angle GFE = \angle DFA$，
∴$\triangle FEG \sim \triangle FAD$.
∴$\frac{FG}{FD} = \frac{EF}{AF}$，即$FG · AF = FD · EF$.
∴$FG = \frac{FD · EF}{AF} = \frac{\sqrt{13}}{26}$.（11分）
[第3步，代值计算结果]
∵$\frac{FG}{DE} = \frac{\frac{\sqrt{13}}{26}}{2} = \frac{\sqrt{13}}{52}$.（12分）
（解析人：王文江）