第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
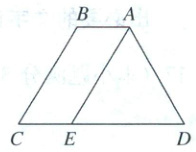
20. (本小题满分 8 分)已知:如图,在梯形$ABCD$中,$AB// CD$,$AD = BC$,$E$是$CD$上一点,且$CE = AB$,$\angle D = 60^{\circ}$.
求证:(1)四边形$ABCE$是平行四边形.
(2)$\triangle AED$是等边三角形.
求证:(1)四边形$ABCE$是平行四边形.
(2)$\triangle AED$是等边三角形.

答案:
20.平行四边形的判定与性质+等边三角形的判定
证明:
(1)
∵$AB//CE$,$AB = CE$,
∴四边形ABCE为平行四边形。
(2)由
(1)可知,四边形ABCE为平行四边形,
∴$AE = BC$。
∵$AD = BC$,
∴$AD = AE$。
∵$∠D = 60°$,
∴$△AED$是等边三角形。
证明:
(1)
∵$AB//CE$,$AB = CE$,
∴四边形ABCE为平行四边形。
(2)由
(1)可知,四边形ABCE为平行四边形,
∴$AE = BC$。
∵$AD = BC$,
∴$AD = AE$。
∵$∠D = 60°$,
∴$△AED$是等边三角形。
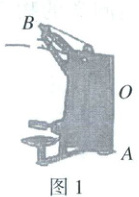
21. (本小题满分 8 分)如图 1 是背肌训练器实物图,图 2、图 3 都是这个训练器在被使用过程中的示意图,立柱$OA$竖直固定在水平地面上,摆臂$OB$可绕点$O$在一定范围内上下转动,$OB$的长为 0.8 米.
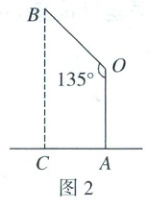
(1)如图 2,$\angle AOB = 135^{\circ}$,握手点$B$离水平地面的竖直高度$BC$为 1.7 米,求立柱$OA$的长(结果精确到 0.1 米).
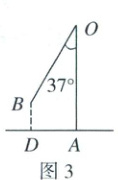
(2)在(1)的条件下,小滨将摆臂$OB$绕点$O$往下拉,若握手点$B$离水平地面的竖直高度不超过 0.6 米,称此次训练为他的“有效训练”.现小滨将摆臂下拉到图 3 位置,$\angle AOB = 37^{\circ}$,请通过计算判断此次训练是否为“有效训练”?
参考数据:$\sin 37^{\circ}\approx 0.60$,$\cos 37^{\circ}\approx 0.80$,$\tan 37^{\circ}\approx 0.75$,$\sqrt{2}\approx 1.414$.
(1)如图 2,$\angle AOB = 135^{\circ}$,握手点$B$离水平地面的竖直高度$BC$为 1.7 米,求立柱$OA$的长(结果精确到 0.1 米).
(2)在(1)的条件下,小滨将摆臂$OB$绕点$O$往下拉,若握手点$B$离水平地面的竖直高度不超过 0.6 米,称此次训练为他的“有效训练”.现小滨将摆臂下拉到图 3 位置,$\angle AOB = 37^{\circ}$,请通过计算判断此次训练是否为“有效训练”?
参考数据:$\sin 37^{\circ}\approx 0.60$,$\cos 37^{\circ}\approx 0.80$,$\tan 37^{\circ}\approx 0.75$,$\sqrt{2}\approx 1.414$.



答案:
21.解直角三角形的应用
解:
(1)如图1,过点O作OP⊥BC于点P。易知四边形AOPC是矩形,则$OA = PC$,$∠AOP = 90°$。

∵$∠AOB = 135°$,
∴$∠BOP = 45°$。
在$Rt△POB$中,$sin∠POB = \frac{BP}{OB}$,
∴$BP = OB·sin∠POB = 0.8×\frac{\sqrt{2}}{2} = 0.4×\sqrt{2} ≈ 0.57$。
∴$OA = BC - BP = 1.7 - 0.57 ≈ 1.1$。
答:立柱OA的长约为1.1米。
(2)如图2,过点B作BM⊥OA于点M。易知四边形BDAM是矩形,则$BD = AM$。

在$Rt△BOM$中,$cos∠MOB = \frac{OM}{OB}$,
∴$OM = OB·cos∠MOB = 0.8×cos37° ≈ 0.8×0.8 = 0.64$。
∴$BD = OA - OM ≈ 1.1 - 0.64 = 0.46$。
∵$0.46 < 0.6$,
∴此次训练是“有效训练”。
21.解直角三角形的应用
解:
(1)如图1,过点O作OP⊥BC于点P。易知四边形AOPC是矩形,则$OA = PC$,$∠AOP = 90°$。

∵$∠AOB = 135°$,
∴$∠BOP = 45°$。
在$Rt△POB$中,$sin∠POB = \frac{BP}{OB}$,
∴$BP = OB·sin∠POB = 0.8×\frac{\sqrt{2}}{2} = 0.4×\sqrt{2} ≈ 0.57$。
∴$OA = BC - BP = 1.7 - 0.57 ≈ 1.1$。
答:立柱OA的长约为1.1米。
(2)如图2,过点B作BM⊥OA于点M。易知四边形BDAM是矩形,则$BD = AM$。

在$Rt△BOM$中,$cos∠MOB = \frac{OM}{OB}$,
∴$OM = OB·cos∠MOB = 0.8×cos37° ≈ 0.8×0.8 = 0.64$。
∴$BD = OA - OM ≈ 1.1 - 0.64 = 0.46$。
∵$0.46 < 0.6$,
∴此次训练是“有效训练”。
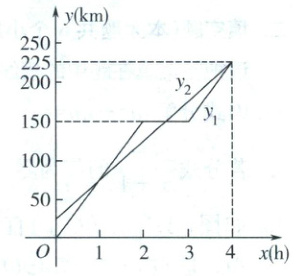
22. (本小题满分 10 分)甲、乙两车分别从相距 225 km 的 A,B 两地相向而行,乙车比甲车先出发半个小时,两车分别以各自的速度匀速行驶.甲在途经 C 地(A,B,C 三地在同一直线上)时因有事停留了 1 小时后,按原速度继续前往 B 地,乙车从 B 地直达 A 地,最终两车同时到达各自目的地.甲、乙两车距各自出发地的路程分别记为$y_{1}$(km),$y_{2}$(km),它们与甲车行驶时间$x$(h)的关系如图所示.
(1)求甲、乙两车的速度.
(2)求$y_{2}$关于$x$的函数表达式.
(3)在$0\leqslant x\leqslant 3$范围内,求甲车在出发多长时间后甲车行驶的路程比乙车行驶的路程多 15 km?
(1)求甲、乙两车的速度.
(2)求$y_{2}$关于$x$的函数表达式.
(3)在$0\leqslant x\leqslant 3$范围内,求甲车在出发多长时间后甲车行驶的路程比乙车行驶的路程多 15 km?

答案:
22.一次函数的应用
解:
(1)甲车的速度为$225÷(4 - 1) = 75(km/h)$,
乙车的速度为$225÷(0.5 + 4) = 50(km/h)$。
(2)$y_2$关于$x$的函数表达式为$y_2 = 50x + 25(0 ≤ x ≤ 4)$。
(3)$150÷75 = 2(h)$,
当$0 ≤ x ≤ 2$时,$y_1 = 75x$,
当$2 < x ≤ 3$时,$y_1 = 150$。
当$0 ≤ x ≤ 2$时,由甲车行驶的路程比乙车行驶的路程多$15km$,得$75x - (50x + 25) = 15$,
解得$x = 1.6$,
当$2 < x ≤ 3$时,由甲车行驶的路程比乙车行驶的路程多$15km$,得$150 - (50x + 25) = 15$,
解得$x = 2.2$。
答:在$0 ≤ x ≤ 3$范围内,甲车在出发$1.6h$或$2.2h$后甲车行驶的路程比乙车行驶的路程多$15km$。
解:
(1)甲车的速度为$225÷(4 - 1) = 75(km/h)$,
乙车的速度为$225÷(0.5 + 4) = 50(km/h)$。
(2)$y_2$关于$x$的函数表达式为$y_2 = 50x + 25(0 ≤ x ≤ 4)$。
(3)$150÷75 = 2(h)$,
当$0 ≤ x ≤ 2$时,$y_1 = 75x$,
当$2 < x ≤ 3$时,$y_1 = 150$。
当$0 ≤ x ≤ 2$时,由甲车行驶的路程比乙车行驶的路程多$15km$,得$75x - (50x + 25) = 15$,
解得$x = 1.6$,
当$2 < x ≤ 3$时,由甲车行驶的路程比乙车行驶的路程多$15km$,得$150 - (50x + 25) = 15$,
解得$x = 2.2$。
答:在$0 ≤ x ≤ 3$范围内,甲车在出发$1.6h$或$2.2h$后甲车行驶的路程比乙车行驶的路程多$15km$。
查看更多完整答案,请扫码查看


