第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
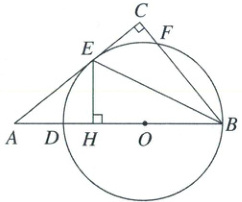
1. 如图,在 $\triangle ABC$ 中,$\angle C = 90^{\circ}$,点 $D$ 是 $AB$ 边上一点,以 $BD$ 为直径的 $\odot O$ 与边 $AC$ 相切于点 $E$,与边 $BC$ 交于点 $F$,过点 $E$ 作 $EH\perp AB$ 于点 $H$,连接 $BE$。
(1) 求证:$BC = BH$。
(2) 若 $AB = 5$,$AC = 4$,求 $CE$ 的长。
(1) 求证:$BC = BH$。
(2) 若 $AB = 5$,$AC = 4$,求 $CE$ 的长。

答案:
1.圆的切线的性质+相似三角形的判定与性质+勾股定理+全等三角形的判定与性质
解:
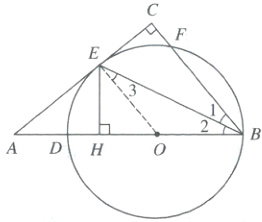
(1)证明:连接$OE$(方法:知切线,连半径),如图
$\because AC$为切线,$\therefore OE \perp AC$。$\therefore \angle AEO = 90^{\circ}$。
$\because \angle C = 90^{\circ}$,$\therefore OE// BC$。$\therefore \angle 1 = \angle 3$。
$\because OB = OE$,$\therefore \angle 2 = \angle 3$。$\therefore \angle 1 = \angle 2$,
$\therefore EH = EC$(提示:角平分线的性质)。
在$Rt\triangle BEH$和$Rt\triangle BEC$中,$\begin{cases}BE = BE,\\EH = EC,\end{cases}$
$\therefore Rt\triangle BEH \cong Rt\triangle BEC(HL)$。$\therefore BC = BH$。
(2)在$Rt\triangle ABC$中,$BC = \sqrt{5^{2} - 4^{2}} = 3$,
设$OE = r$,则$AO = 5 - r$。
$\because OE// BC$,$\therefore \triangle AOE \sim \triangle ABC$。
$\therefore \frac{AO}{AB} = \frac{OE}{BC}$,即$\frac{5 - r}{5} = \frac{r}{3}$,
解得$r = \frac{15}{8}$。
$\therefore AO = 5 - r = \frac{25}{8}$。
在$Rt\triangle AOE$中,$AE = \sqrt{(\frac{25}{8})^{2} - (\frac{15}{8})^{2}} = \frac{5}{2}$,
$\therefore CE = AC - AE = 4 - \frac{5}{2} = \frac{3}{2}$。
1.圆的切线的性质+相似三角形的判定与性质+勾股定理+全等三角形的判定与性质
解:
(1)证明:连接$OE$(方法:知切线,连半径),如图
$\because AC$为切线,$\therefore OE \perp AC$。$\therefore \angle AEO = 90^{\circ}$。
$\because \angle C = 90^{\circ}$,$\therefore OE// BC$。$\therefore \angle 1 = \angle 3$。
$\because OB = OE$,$\therefore \angle 2 = \angle 3$。$\therefore \angle 1 = \angle 2$,
$\therefore EH = EC$(提示:角平分线的性质)。
在$Rt\triangle BEH$和$Rt\triangle BEC$中,$\begin{cases}BE = BE,\\EH = EC,\end{cases}$
$\therefore Rt\triangle BEH \cong Rt\triangle BEC(HL)$。$\therefore BC = BH$。

(2)在$Rt\triangle ABC$中,$BC = \sqrt{5^{2} - 4^{2}} = 3$,
设$OE = r$,则$AO = 5 - r$。
$\because OE// BC$,$\therefore \triangle AOE \sim \triangle ABC$。
$\therefore \frac{AO}{AB} = \frac{OE}{BC}$,即$\frac{5 - r}{5} = \frac{r}{3}$,
解得$r = \frac{15}{8}$。
$\therefore AO = 5 - r = \frac{25}{8}$。
在$Rt\triangle AOE$中,$AE = \sqrt{(\frac{25}{8})^{2} - (\frac{15}{8})^{2}} = \frac{5}{2}$,
$\therefore CE = AC - AE = 4 - \frac{5}{2} = \frac{3}{2}$。
2. 如图,已知 $AB$ 是 $\odot O$ 的直径,$C$ 为 $\odot O$ 上一点,连接 $AC$,$BC$,$D$ 为 $AC$ 上一点,连接 $DB$ 并延长交过 $C$ 点 $\odot O$ 的切线于点 $E$,已知 $CD = CB$。
(1) 求证:$\angle ABD=\angle E$。
(2) 若 $AB = 13$,$AD = 7$,求 $CE$ 长。

(1) 求证:$\angle ABD=\angle E$。
(2) 若 $AB = 13$,$AD = 7$,求 $CE$ 长。

答案:
2.圆的切线的性质+圆的性质+相似三角形的判定与性质+勾股定理
解:
(1)证明:如图,连接$OC$(巧作辅助线:连接半径,根据切线的性质得到直角)。

$\because CE$为$\odot O$的切线,$\therefore OC \perp CE$。
$\therefore \angle ECB + \angle OCB = 90^{\circ}$。
$\because AB$为$\odot O$的直径,
$\therefore \angle ACB = 90^{\circ}$。
$\therefore \angle ACO + \angle OCB = 90^{\circ}$。
$\therefore \angle ECB = \angle ACO$。
又$OC = OA$,
$\therefore \angle OAC = \angle OCA = \angle ECB$。
$\because CD = CB$,
$\therefore \angle CDB = \angle CBD = 45^{\circ}$。
$\therefore \angle OAC + \angle ABD = \angle ECB + \angle E = 45^{\circ}$。
$\therefore \angle ABD = \angle E$。
(2)设$BC = CD = x$。
在$Rt\triangle ABC$中,$x^{2} + (7 + x)^{2} = 13^{2}$,
解得$x = 5$,
$\therefore BC = 5$。
由
(1)知$\angle ABD = \angle E$,$\angle DAB = \angle BCE$,
$\therefore \triangle ADB \sim \triangle CBE$。
$\therefore \frac{AD}{BC} = \frac{AB}{CE}$,即$\frac{7}{5} = \frac{13}{CE}$,
解得$CE = \frac{65}{7}$。
2.圆的切线的性质+圆的性质+相似三角形的判定与性质+勾股定理
解:
(1)证明:如图,连接$OC$(巧作辅助线:连接半径,根据切线的性质得到直角)。

$\because CE$为$\odot O$的切线,$\therefore OC \perp CE$。
$\therefore \angle ECB + \angle OCB = 90^{\circ}$。
$\because AB$为$\odot O$的直径,
$\therefore \angle ACB = 90^{\circ}$。
$\therefore \angle ACO + \angle OCB = 90^{\circ}$。
$\therefore \angle ECB = \angle ACO$。
又$OC = OA$,
$\therefore \angle OAC = \angle OCA = \angle ECB$。
$\because CD = CB$,
$\therefore \angle CDB = \angle CBD = 45^{\circ}$。
$\therefore \angle OAC + \angle ABD = \angle ECB + \angle E = 45^{\circ}$。
$\therefore \angle ABD = \angle E$。
(2)设$BC = CD = x$。
在$Rt\triangle ABC$中,$x^{2} + (7 + x)^{2} = 13^{2}$,
解得$x = 5$,
$\therefore BC = 5$。
由
(1)知$\angle ABD = \angle E$,$\angle DAB = \angle BCE$,
$\therefore \triangle ADB \sim \triangle CBE$。
$\therefore \frac{AD}{BC} = \frac{AB}{CE}$,即$\frac{7}{5} = \frac{13}{CE}$,
解得$CE = \frac{65}{7}$。
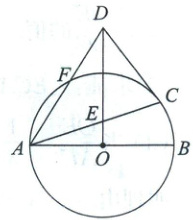
3. 如图,$AB$ 是 $\odot O$ 的直径,$CD$ 是 $\odot O$ 的切线,$C$ 为切点,$OD\perp AB$ 于点 $O$,与 $AC$ 交于点 $E$。
(1) 求证:$DE = DC$。
(2) 连接 $AD$ 与 $\odot O$ 相交于点 $F$,若 $\odot O$ 的半径为 $3$,$OE = 1$,求点 $O$ 到 $AD$ 的距离。
(1) 求证:$DE = DC$。
(2) 连接 $AD$ 与 $\odot O$ 相交于点 $F$,若 $\odot O$ 的半径为 $3$,$OE = 1$,求点 $O$ 到 $AD$ 的距离。

答案:
3.圆的切线的性质+等腰三角形的性质+勾股定理+三角函数的概念
解:
(1)证明:如图,连接$OC$(巧作辅助线:构造等腰三角形求解),
$\because OC = OA$,
$\therefore \angle OCA = \angle OAC$。
$\because CD$是$\odot O$的切线,
$\therefore CD \perp OC$(提醒:切线垂直于过切点的半径)。
$\therefore \angle OCA + \angle DCE = \angle OCD = 90^{\circ}$。
$\because OD \perp AB$于点$O$,
$\therefore \angle AOD = 90^{\circ}$。
$\because \angle DEC = \angle AEO$,
$\therefore \angle OAC + \angle DEC = \angle OAC + \angle AEO = 90^{\circ}$。
$\therefore \angle DCE = \angle DEC$。
$\therefore DE = DC$。

(2)如图,作$OG \perp AD$于点$G$,则$\angle AGO = 90^{\circ}$(巧作辅助线:作垂线,构造直角三角形,利用锐角三角函数求解)。
$\because \odot O$的半径为$3$,
$\therefore OA = OC = 3$。
$\because OC^{2} + DC^{2} = OD^{2}$,且$DC = DE$,$OD = 1 + DE$,
$\therefore 3^{2} + DE^{2} = (1 + DE)^{2}$,解得$DE = 4$。
$\therefore OD = 1 + 4 = 5$。
$\therefore AD = \sqrt{OA^{2} + OD^{2}} = \sqrt{3^{2} + 5^{2}} = \sqrt{34}$。
$\because \frac{OG}{OA} = \frac{OD}{AD} = \sin\angle OAD$,
$\therefore OG = \frac{OA · OD}{AD} = \frac{3 × 5}{\sqrt{34}} = \frac{15\sqrt{34}}{34}$。
$\therefore$点$O$到$AD$的距离为$\frac{15\sqrt{34}}{34}$。
3.圆的切线的性质+等腰三角形的性质+勾股定理+三角函数的概念
解:
(1)证明:如图,连接$OC$(巧作辅助线:构造等腰三角形求解),
$\because OC = OA$,
$\therefore \angle OCA = \angle OAC$。
$\because CD$是$\odot O$的切线,
$\therefore CD \perp OC$(提醒:切线垂直于过切点的半径)。
$\therefore \angle OCA + \angle DCE = \angle OCD = 90^{\circ}$。
$\because OD \perp AB$于点$O$,
$\therefore \angle AOD = 90^{\circ}$。
$\because \angle DEC = \angle AEO$,
$\therefore \angle OAC + \angle DEC = \angle OAC + \angle AEO = 90^{\circ}$。
$\therefore \angle DCE = \angle DEC$。
$\therefore DE = DC$。

(2)如图,作$OG \perp AD$于点$G$,则$\angle AGO = 90^{\circ}$(巧作辅助线:作垂线,构造直角三角形,利用锐角三角函数求解)。
$\because \odot O$的半径为$3$,
$\therefore OA = OC = 3$。
$\because OC^{2} + DC^{2} = OD^{2}$,且$DC = DE$,$OD = 1 + DE$,
$\therefore 3^{2} + DE^{2} = (1 + DE)^{2}$,解得$DE = 4$。
$\therefore OD = 1 + 4 = 5$。
$\therefore AD = \sqrt{OA^{2} + OD^{2}} = \sqrt{3^{2} + 5^{2}} = \sqrt{34}$。
$\because \frac{OG}{OA} = \frac{OD}{AD} = \sin\angle OAD$,
$\therefore OG = \frac{OA · OD}{AD} = \frac{3 × 5}{\sqrt{34}} = \frac{15\sqrt{34}}{34}$。
$\therefore$点$O$到$AD$的距离为$\frac{15\sqrt{34}}{34}$。
查看更多完整答案,请扫码查看


