《2026年天利38套中考试题精选数学浙江专版》

8. 数学综合与实践活动小组用四个全等的直角三角形（$ Rt \triangle AHB \cong Rt \triangle BEC \cong Rt \triangle CFD \cong Rt \triangle DGA $）拼成如图所示的“赵爽弦图”，得到正方形 $ ABCD $ 和正方形 $ EFGH $，连接 $ AC $ 和 $ EG $，$ AC $ 与 $ DF $，$ EG $，$ BH $ 分别相交于点 $ P $，$ O $，$ Q $。若 $ \frac{BE}{QE} = \frac{14}{15} $，则 $ \frac{OP}{OE} $ 的值是__________。

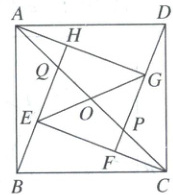
$\frac {\sqrt {29}}{7}$

答案： 8 $\frac {\sqrt {29}}{7}$

1. 如图，正比例函数 $ y_1 = -3x $ 的图象与反比例函数 $ y_2 = \frac{k}{x} $ 的图象交于 $ A $，$ B $ 两点。点 $ C $ 在 $ x $ 轴负半轴上，$ AC = AO $，$ \triangle ACO $ 的面积为 12，则 $ k = $-12。

答案： 1 -12

2. 如图，$ A $，$ B $ 是反比例函数 $ y = \frac{12}{x} $ 图象上的两点，过点 $ A $ 作 $ AC \perp y $ 轴，垂足为 $ C $，$ AC $ 交 $ OB $ 于点 $ D $。若 $ D $ 为 $ OB $ 的中点，则 $ \triangle ABD $ 的面积为__________。

$\frac {9}{2}$

答案： 2 $\frac {9}{2}$

3. 二次函数 $ y = ax^2 - 2ax + 2 $（$ a ＜ 0 $）的图象过 $ A(-1, y_1) $，$ B(1, y_2) $，$ C(4, y_3) $ 三个点。若 $ y_1y_2y_3 ＜ 0 $，则 $ a $ 的取值范围是$-\frac {2}{3}＜a＜-\frac {1}{4}$。

答案： 3 $-\frac {2}{3}＜a＜-\frac {1}{4}$

4. 在平面直角坐标系 $ xOy $ 中，点 $ A(a, b) $（$ a ＞ 0 $，$ b ＞ 0 $）在双曲线 $ y = \frac{k_1}{x} $ 上，点 $ A $ 关于 $ x $ 轴对称的点 $ B $ 在双曲线 $ y = \frac{k_2}{x} $，则 $ k_1 + k_2 $ 的值为0。

答案： 4 0

5. 已知抛物线 $ y = x^2 + 2x - n $ 与 $ x $ 轴交于 $ A $，$ B $ 两点，抛物线 $ y = x^2 - 2x - n $ 与 $ x $ 轴交于 $ C $，$ D $ 两点，其中 $ n ＞ 0 $。若 $ AD = 2BC $，则 $ n $ 的值为5 8。

答案： 5 8

6. 如图，点 $ A $ 是双曲线 $ y = \frac{6}{x} $（$ x ＞ 0 $）上的动点，过点 $ A $ 作 $ x $ 轴的平行线交双曲线 $ y = \frac{k}{x} $ 于点 $ B $，作 $ AC \perp x $ 轴于点 $ C $，连接 $ BC $，若四边形 $ OABC $ 为平行四边形，则 $ k $ 的值是-6。

答案： 6 12

7. 对于二次函数 $ y = x^2 - 4ax + a^2 + 1 $，当 $ x \geq 2 $ 时，$ y $ 随 $ x $ 的增大而增大。已知此二次函数的图象上有一点 $ A(1, m) $，则 $ m $ 的取值范围为m≥-1。

答案： m≥-1

1. 如图，$ \triangle ABC $ 内接于 $ \odot O $，过点 $ B $ 作 $ \odot O $ 的切线 $ BD $，$ \triangle BCE $ 为直角三角形，且 $ \angle BCE = 90° $。若 $ BE = 5 $，$ EC = 4 $，则 $ \odot O $ 的半径为$\frac {15}{8}$。

答案： 1 $\frac {15}{8}$

2. 如图，四边形 $ ABCD $ 是 $ \odot O $ 的内接四边形，$ AB = AD $，直线 $ MN $ 与 $ \odot O $ 相切于点 $ A $。若 $ \angle MAD = 40° $，则 $ \angle C $ 的大小为80度。

答案： 2 80