第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 某种筷子的合格长度标准为 $ 240\ mm \pm 2\ mm $,则下列四双筷子中合格的长度是(
A.$ 235\ mm $
B.$ 239\ mm $
C.$ 243\ mm $
D.$ 245\ mm $
B
)A.$ 235\ mm $
B.$ 239\ mm $
C.$ 243\ mm $
D.$ 245\ mm $
答案:
1. B【考点】有理数的加法 + 有理数的减法
2. 下列图形中,既是轴对称图形又是中心对称图形的是(
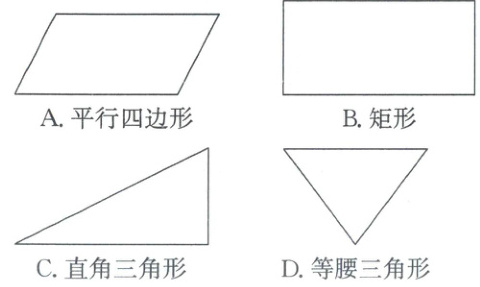
B
)
答案:
2. B【考点】中心对称图形 + 轴对称图形
3. 下列运算正确的是(
A.$ a^{2} · a^{3} = a^{6} $
B.$ (-3a)^{2} = -9a^{2} $
C.$ (-a)^{6} ÷ a^{3} = a^{3} $
D.$ (a - b)^{2} = a^{2} - b^{2} $
C
)A.$ a^{2} · a^{3} = a^{6} $
B.$ (-3a)^{2} = -9a^{2} $
C.$ (-a)^{6} ÷ a^{3} = a^{3} $
D.$ (a - b)^{2} = a^{2} - b^{2} $
答案:
3. C【解析】完全平方公式 + 同底数幂的乘法 + 积的乘方 + 同底数幂的除法
选项 逐项分析 正误
A $a^2· a^3=a^5$ ×
B $(-3a)^2=9a^2$ ×
C $(-a)^6÷ a^3=a^6÷ a^3=a^3$ √
D $(a - b)^2=a^2 - 2ab + b^2$ ×
故选C。
选项 逐项分析 正误
A $a^2· a^3=a^5$ ×
B $(-3a)^2=9a^2$ ×
C $(-a)^6÷ a^3=a^6÷ a^3=a^3$ √
D $(a - b)^2=a^2 - 2ab + b^2$ ×
故选C。
4. 小聪和小明5次数学测验的成绩如表,若小聪的平均分高于小明,则 $ a $ 的值可取(
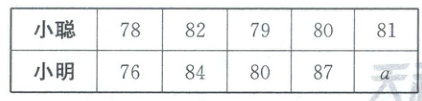
A.75
B.74
C.73
D.72
D
)
A.75
B.74
C.73
D.72
答案:
4. D【解析】平均数 + 解一元一次不等式 由题表可得,小聪的平均分为$\frac{78 + 82 + 79 + 80 + 81}{5}=80$,$\because$小聪的平均分高于小明,$\therefore \frac{76 + 84 + 80 + 87 + a}{5}<80$。解得$a<73$。$\therefore a$可以是72。故选D。
5. 如图,$ \triangle ABC $ 的三个顶点都在 $ 3 × 1 $ 的正方形网格的格点上,则 $ \tan B $ 的值为( )
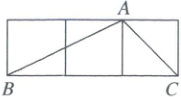
A.$ \frac{1}{2} $
B.$ \frac{\sqrt{5}}{5} $
C.$ \frac{\sqrt{10}}{5} $
D.$ \frac{2\sqrt{5}}{5} $

A.$ \frac{1}{2} $
B.$ \frac{\sqrt{5}}{5} $
C.$ \frac{\sqrt{10}}{5} $
D.$ \frac{2\sqrt{5}}{5} $
答案:
5. A【解析】锐角三角函数的定义 如图所示,设小正方形的边长为$a$,在$\mathrm{Rt}\triangle ABM$中,$\tan B=\frac{AM}{BM}=\frac{\frac{a}{2}}{2a}=\frac{1}{2}$。故选A。

5. A【解析】锐角三角函数的定义 如图所示,设小正方形的边长为$a$,在$\mathrm{Rt}\triangle ABM$中,$\tan B=\frac{AM}{BM}=\frac{\frac{a}{2}}{2a}=\frac{1}{2}$。故选A。

6. 不等式 $ 3(x - 1) \geq 6 $ 的解集是(
A.$ x \geq 1 $
B.$ x \leq 1 $
C.$ x \geq 3 $
D.$ x \leq 3 $
C
)A.$ x \geq 1 $
B.$ x \leq 1 $
C.$ x \geq 3 $
D.$ x \leq 3 $
答案:
6. C【解析】解一元一次不等式 $\because 3(x - 1)\geq6$,$\therefore x - 1\geq2$。$\therefore x\geq3$。故选C。
7. 平面直角坐标系 $ xOy $ 中,点 $ A $ 的坐标为 $ (3, \sqrt{3}) $,将线段 $ OA $ 绕点 $ O $ 逆时针旋转 $ 60^{\circ} $,则点 $ A $ 的对应点 $ A' $ 的坐标为( )
A.$ (-1, 2\sqrt{3}) $
B.$ (0, 2\sqrt{3}) $
C.$ (-1, 3) $
D.$ (0, 3) $
A.$ (-1, 2\sqrt{3}) $
B.$ (0, 2\sqrt{3}) $
C.$ (-1, 3) $
D.$ (0, 3) $
答案:
7. B【解析】平面直角坐标系中点的坐标特征 + 旋转 如图,过点A作$AB\perp x$轴于点B。$\because$点A的坐标为$(3,\sqrt{3})$,$\therefore OB = 3$,$AB = \sqrt{3}$。$\therefore OA = \sqrt{3^2 + (\sqrt{3})^2}=2\sqrt{3}$。$\therefore OA = 2AB$。$\therefore \angle AOB = 30°$。$\because$线段OA绕点O逆时针旋转$60°$得到$OA'$,$\therefore OA' = OA = 2\sqrt{3}$,$\angle AOA' = 60°$。$\therefore \angle BOA' = \angle AOB + \angle AOA' = 90°$。$\therefore$点A'在y轴正半轴上。$\therefore$点A的对应点A'的坐标为$(0,2\sqrt{3})$。故选B。

7. B【解析】平面直角坐标系中点的坐标特征 + 旋转 如图,过点A作$AB\perp x$轴于点B。$\because$点A的坐标为$(3,\sqrt{3})$,$\therefore OB = 3$,$AB = \sqrt{3}$。$\therefore OA = \sqrt{3^2 + (\sqrt{3})^2}=2\sqrt{3}$。$\therefore OA = 2AB$。$\therefore \angle AOB = 30°$。$\because$线段OA绕点O逆时针旋转$60°$得到$OA'$,$\therefore OA' = OA = 2\sqrt{3}$,$\angle AOA' = 60°$。$\therefore \angle BOA' = \angle AOB + \angle AOA' = 90°$。$\therefore$点A'在y轴正半轴上。$\therefore$点A的对应点A'的坐标为$(0,2\sqrt{3})$。故选B。

8. 《九章算术》中记载了这样一个问题:“今有共买物,人出八,盈三;人出七,不足四. 问人数、物价各几何?”设共有 $ x $ 人,用不同的代数式表示物品价格,可得到方程(
A.$ 8x - 3 = 7x - 4 $
B.$ 8x + 3 = 7x - 4 $
C.$ 8x - 3 = 7x + 4 $
D.$ 8x + 3 = 7x + 4 $
8x - 3 = 7x + 4
)A.$ 8x - 3 = 7x - 4 $
B.$ 8x + 3 = 7x - 4 $
C.$ 8x - 3 = 7x + 4 $
D.$ 8x + 3 = 7x + 4 $
答案:
8. C【解析】由实际问题抽象出一元一次方程 由题知共有$x$人,根据“人出八,盈三;人出七,不足四”,并结合物品的价格不变,可得方程$8x - 3 = 7x + 4$。故选C。
9. 如图,是三个反比例函数 $ y = \frac{k_{1}}{x} $,$ y = \frac{k_{2}}{x} $,$ y = \frac{k_{3}}{x} $ 在 $ x $ 轴上方的图象,则 $ k_{1} $,$ k_{2} $,$ k_{3} $ 的大小关系为(
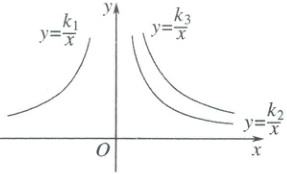
A.$ k_{1} < k_{2} < k_{3} $
B.$ k_{1} < k_{3} < k_{2} $
C.$ k_{2} < k_{1} < k_{3} $
D.$ k_{2} < k_{3} < k_{1} $
A
)
A.$ k_{1} < k_{2} < k_{3} $
B.$ k_{1} < k_{3} < k_{2} $
C.$ k_{2} < k_{1} < k_{3} $
D.$ k_{2} < k_{3} < k_{1} $
答案:
9. A【解析】反比例函数的图象与性质 由三个反比例函数的图象可知$k_1<0$,$k_3>k_2>0$,所以$k_1<k_2<k_3$。故选A。
10. 如图,在菱形 $ ABCD $ 中,$ DE \perp BA $,交 $ BA $ 的延长线于点 $ E $,$ EF \perp BC $ 于点 $ F $,若 $ \frac{BF}{BE} = \frac{2}{5} $,四边形 $ BCDE $ 的面积为 $ 12\sqrt{21} $,则 $ BF $ 的长为(
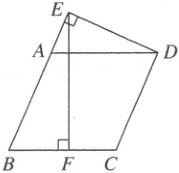
A.$ \sqrt{7} $
B.$ \sqrt{21} $
C.$ \frac{14}{5} $
D.$ \frac{14\sqrt{2}}{5} $
D
)
A.$ \sqrt{7} $
B.$ \sqrt{21} $
C.$ \frac{14}{5} $
D.$ \frac{14\sqrt{2}}{5} $
答案:
10. D【解析】菱形的性质 + 相似三角形的判定与性质 + 梯形的面积公式 + 勾股定理
[第1步,利用已知条件及相似三角形的判定与性质得到$\frac{AE}{AD}=\frac{2}{5}$]
$\because DE\perp BA$,交BA的延长线于点E,$EF\perp BC$于点F,$\therefore \angle AED = \angle BFE = 90°$。$\because$四边形ABCD是菱形,$\therefore AD// BC$,$AD = AB = CD$。$\therefore \angle EAD = \angle B$。$\therefore \triangle AED\sim \triangle BFE$。
$\therefore \frac{AE}{BF}=\frac{AD}{BE}$(提示:相似三角形的判定与性质)。$\therefore \frac{AE}{AD}=\frac{BF}{BE}=\frac{2}{5}$。
[第2步,利用勾股定理和线段的和差得出DE,BE的长度]
设$AD = AB = CD = 5n$,则$AE = \frac{2}{5}AD = 2n$。$\therefore DE = \sqrt{AD^2 - AE^2}=\sqrt{(5n)^2 - (2n)^2}=\sqrt{21}n$,$BE = AB + AE = 7n$。
[第3步,利用梯形的面积公式得到BE的长度,进而得出BF的长度]
$\because CD// BE$,$DE\perp BE$,$\therefore$四边形BCDE是直角梯形。$\therefore S_{梯形BCDE}=\frac{1}{2}DE(CD + BE)=12\sqrt{21}$。$\therefore \frac{1}{2}× \sqrt{21}n×(5n + 7n)=12\sqrt{21}$,解得$n_1 = \sqrt{2}$,$n_2 = -\sqrt{2}$(舍去)。$\therefore BE = 7\sqrt{2}$。$\therefore BF = \frac{2}{5}BE = \frac{2}{5}× 7\sqrt{2}=\frac{14\sqrt{2}}{5}$。故选D。
[第1步,利用已知条件及相似三角形的判定与性质得到$\frac{AE}{AD}=\frac{2}{5}$]
$\because DE\perp BA$,交BA的延长线于点E,$EF\perp BC$于点F,$\therefore \angle AED = \angle BFE = 90°$。$\because$四边形ABCD是菱形,$\therefore AD// BC$,$AD = AB = CD$。$\therefore \angle EAD = \angle B$。$\therefore \triangle AED\sim \triangle BFE$。
$\therefore \frac{AE}{BF}=\frac{AD}{BE}$(提示:相似三角形的判定与性质)。$\therefore \frac{AE}{AD}=\frac{BF}{BE}=\frac{2}{5}$。
[第2步,利用勾股定理和线段的和差得出DE,BE的长度]
设$AD = AB = CD = 5n$,则$AE = \frac{2}{5}AD = 2n$。$\therefore DE = \sqrt{AD^2 - AE^2}=\sqrt{(5n)^2 - (2n)^2}=\sqrt{21}n$,$BE = AB + AE = 7n$。
[第3步,利用梯形的面积公式得到BE的长度,进而得出BF的长度]
$\because CD// BE$,$DE\perp BE$,$\therefore$四边形BCDE是直角梯形。$\therefore S_{梯形BCDE}=\frac{1}{2}DE(CD + BE)=12\sqrt{21}$。$\therefore \frac{1}{2}× \sqrt{21}n×(5n + 7n)=12\sqrt{21}$,解得$n_1 = \sqrt{2}$,$n_2 = -\sqrt{2}$(舍去)。$\therefore BE = 7\sqrt{2}$。$\therefore BF = \frac{2}{5}BE = \frac{2}{5}× 7\sqrt{2}=\frac{14\sqrt{2}}{5}$。故选D。
查看更多完整答案,请扫码查看


