第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
11. 2025 年杭州市参加中考人数约为 41 000,将 41 000 用科学记数法表示为
$4.1 × 10^{4}$
.
答案:
11. $4.1 × 10^{4}$ [考点]科学记数法
12. “宫商角徵羽”是中国古乐的五个基本音阶(相当于西乐的 1,2,3,5,6),是采用“三分损益法”获得的. 如图,现有一款“一起听古音”的音乐玩具,音乐小球从$A$处沿轨道进入小洞就可以发出相应的声音,且小球进入每个小洞的可能性相同,现有音乐小球从$A$处进入小洞发出“羽”音的概率是
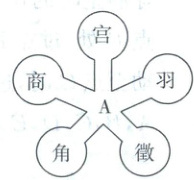
$\frac{1}{5}$
.
答案:
12 $\frac{1}{5}$
13. 如图,$A,B,C$是$\odot O$上的点,$\angle C=30^{\circ},OA=2$,则$\overgroup{AB}$的长为
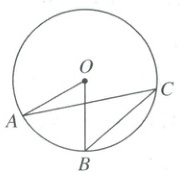
$\frac{2}{3}\pi$
(结果保留$\pi$).
答案:
13 $\frac{2}{3} \pi$ [解析]圆周角定理+弧长公式 $\because \angle C = 30^{\circ}$,$\therefore \angle AOB = 2\angle C = 60^{\circ}$.$\because OA = 2$,$\therefore AB$的长为$\frac{60}{180} \pi × 2 = \frac{2}{3} \pi$.
14. 将公式$y=\frac{1-x}{x}$变形成用$y$表示$x$,则$x=$
$\frac{1}{y+1}$
.
答案:
14 $\frac{1}{y+1}$ [解析]等式的变形
解法一(倒数法):$\because y = \frac{1 - x}{x} = \frac{1}{x} - \frac{x}{x} = \frac{1}{x} - 1$,$\therefore \frac{1}{x} = y + 1$.$\therefore x = \frac{1}{y+1}$.
解法二(等式性质法):$\because y = \frac{1 - x}{x}$,$\therefore xy = 1 - x$.$\therefore xy + x = 1$.$\therefore x(y + 1) = 1$.$\therefore x = \frac{1}{y+1}$.
解法一(倒数法):$\because y = \frac{1 - x}{x} = \frac{1}{x} - \frac{x}{x} = \frac{1}{x} - 1$,$\therefore \frac{1}{x} = y + 1$.$\therefore x = \frac{1}{y+1}$.
解法二(等式性质法):$\because y = \frac{1 - x}{x}$,$\therefore xy = 1 - x$.$\therefore xy + x = 1$.$\therefore x(y + 1) = 1$.$\therefore x = \frac{1}{y+1}$.
15. 春节假期小明一家自驾车从杭州到离家约 900 km 的青岛旅游,出发前将油箱加满油. 下表记录了轿车行驶的路程$x$(km)与油箱剩余油量$y$(L)之间的部分数据:

若该轿车满油为 50 L,假设该轿车正常行驶时每千米耗油量相同,油箱内至少要有 5 L 及以上汽油才能保证汽车正常行驶,则小明家的轿车至多开

若该轿车满油为 50 L,假设该轿车正常行驶时每千米耗油量相同,油箱内至少要有 5 L 及以上汽油才能保证汽车正常行驶,则小明家的轿车至多开
562.5
km 就必须去加油.
答案:
15 562.5 [解析]一次函数的应用 根据题表中的数据可得油箱剩余油量$y$与行驶的路程$x$满足一次函数关系(关键:当路程$x$每增加100km时油箱剩余油量减少8L,因此可得剩余油量$y$与行驶的路程$x$满足一次函数关系).设$y$关于$x$的函数表达式为$y = kx + b(k \neq 0)$.将$(0,50)$,$(100,42)$的坐标代入$y = kx + b$得$\begin{cases} b = 50 \\ 100k + b = 42 \end{cases}$,解得$\begin{cases} k = -0.08 \\ b = 50 \end{cases}$,$\therefore y$关于$x$的函数表达式为$y = -0.08x + 50$.当$y = 5$时,$-0.08x + 50 = 5$,解得$x = 562.5$.$\therefore$小明家的轿车至多开562.5km就必须去加油.
16. 如图,线段$AB$绕点$A$逆时针旋转得到线段$AC,AD$,已知$\angle BAD=108^{\circ}$,连接线段$DC$并延长,与$\angle CAB$的平分线交于点$E$,连接$BE$. 若$AE=DE,DC=1$,则线段$AE$的长为
$\frac{\sqrt{5}+3}{2}$
.zyjl.cn/pic18/2025-11-27/4ecc83a52aa0c1b9c83db73b2aa9cd09.jpg?x-oss-process=image/crop,x_1218,y_0,w_1207,h_1675/crop,x_783,y_115,w_183,h_180" />
答案:
16 $\frac{\sqrt{5}+3}{2}$ [解析]三角形内角和定理+三角形外角的性质+相似三角形的判定与性质
[第1步,利用旋转的性质及三角形外角的性质求出$\angle CEA$的度数]
设$\angle CAE = \alpha$,$\because AE$平分$\angle CAB$,$\therefore \angle BAE = \alpha$.$\because \angle BAD = 108^{\circ}$,$\therefore \angle DAC = 108^{\circ} - 2\alpha$.$\therefore \angle ACD = \frac{180^{\circ} - \angle DAC}{2} = 36^{\circ} + \alpha$.$\because \angle ACD = \angle CAE + \angle CEA$(提示:三角形外角的性质),$\therefore \angle CEA = 36^{\circ}$.
[第2步,结合等腰三角形的性质求出$\angle DAC$,$\angle CAE$的度数]
$\because AE = DE$,$\therefore \angle D = \angle DAE = 72^{\circ}$.$\therefore \angle BAE = 36^{\circ}$.$\therefore \angle CAE = 36^{\circ}$.$\therefore \angle DAC = 36^{\circ}$.
[第3步,证明$\triangle EAD \sim \triangle ACD$,根据相似三角形的性质求出$CE$的长,进而得出$AE$的长]
$\because \angle DAC = \angle CEA = \angle CAE = 36^{\circ}$.$\therefore CE = AC$.又$\because \angle D = \angle D$,$\therefore \triangle EAD \sim \triangle ACD$.$\therefore \frac{AE}{CA} = \frac{AD}{CD}$.设$CE = AC = m$,$\because DC = 1$,$\therefore AE = DE = m + 1$.$\therefore \frac{m + 1}{m} = \frac{m}{1}$.$\therefore m^{2} - m - 1 = 0$,解得$m = \frac{1 + \sqrt{5}}{2}$(舍负).$\therefore AE = m + 1 = \frac{1 + \sqrt{5}}{2} + 1 = \frac{\sqrt{5}+3}{2}$.
知识拓展
黄金三角形
第1类:在等腰三角形中两个底角为$72^{\circ}$,顶角为$36^{\circ}$.这样的三角形的底边长与一腰长之比为黄金比$\frac{\sqrt{5} - 1}{2}$.
第2类:在等腰三角形中两个底角为$36^{\circ}$,顶角为$108^{\circ}$.这样的三角形的一腰长与底边长之比为黄金比$\frac{\sqrt{5} - 1}{2}$.
[第1步,利用旋转的性质及三角形外角的性质求出$\angle CEA$的度数]
设$\angle CAE = \alpha$,$\because AE$平分$\angle CAB$,$\therefore \angle BAE = \alpha$.$\because \angle BAD = 108^{\circ}$,$\therefore \angle DAC = 108^{\circ} - 2\alpha$.$\therefore \angle ACD = \frac{180^{\circ} - \angle DAC}{2} = 36^{\circ} + \alpha$.$\because \angle ACD = \angle CAE + \angle CEA$(提示:三角形外角的性质),$\therefore \angle CEA = 36^{\circ}$.
[第2步,结合等腰三角形的性质求出$\angle DAC$,$\angle CAE$的度数]
$\because AE = DE$,$\therefore \angle D = \angle DAE = 72^{\circ}$.$\therefore \angle BAE = 36^{\circ}$.$\therefore \angle CAE = 36^{\circ}$.$\therefore \angle DAC = 36^{\circ}$.
[第3步,证明$\triangle EAD \sim \triangle ACD$,根据相似三角形的性质求出$CE$的长,进而得出$AE$的长]
$\because \angle DAC = \angle CEA = \angle CAE = 36^{\circ}$.$\therefore CE = AC$.又$\because \angle D = \angle D$,$\therefore \triangle EAD \sim \triangle ACD$.$\therefore \frac{AE}{CA} = \frac{AD}{CD}$.设$CE = AC = m$,$\because DC = 1$,$\therefore AE = DE = m + 1$.$\therefore \frac{m + 1}{m} = \frac{m}{1}$.$\therefore m^{2} - m - 1 = 0$,解得$m = \frac{1 + \sqrt{5}}{2}$(舍负).$\therefore AE = m + 1 = \frac{1 + \sqrt{5}}{2} + 1 = \frac{\sqrt{5}+3}{2}$.
知识拓展
黄金三角形
第1类:在等腰三角形中两个底角为$72^{\circ}$,顶角为$36^{\circ}$.这样的三角形的底边长与一腰长之比为黄金比$\frac{\sqrt{5} - 1}{2}$.
第2类:在等腰三角形中两个底角为$36^{\circ}$,顶角为$108^{\circ}$.这样的三角形的一腰长与底边长之比为黄金比$\frac{\sqrt{5} - 1}{2}$.
17. (本小题满分 8 分)
(1)计算:$2 025^{0}-(\frac{1}{2})^{-1}+\sqrt{9}$.
(2)化简:$(x-1)^{2}-x(x-2)$.
(1)计算:$2 025^{0}-(\frac{1}{2})^{-1}+\sqrt{9}$.
(2)化简:$(x-1)^{2}-x(x-2)$.
答案:
17. 实数的运算+整式的化简
解:
(1)原式$= 1 - 2 + 3$
$= 2$.
(2)原式$= x^{2} - 2x + 1 - x^{2} + 2x$[提醒:完全平方公式:$(a \pm b)^{2} = a^{2} \pm 2ab + b^{2}$]
$= 1$.
解:
(1)原式$= 1 - 2 + 3$
$= 2$.
(2)原式$= x^{2} - 2x + 1 - x^{2} + 2x$[提醒:完全平方公式:$(a \pm b)^{2} = a^{2} \pm 2ab + b^{2}$]
$= 1$.
18. (本小题满分 8 分)解方程:
(1)$3(x-1)-2x=-6$.
(2)$\frac{x}{x+1}+\frac{3}{x}=1$.
(1)$3(x-1)-2x=-6$.
(2)$\frac{x}{x+1}+\frac{3}{x}=1$.
答案:
18. 解一元一次方程+解分式方程
解:
(1)$3(x - 1) - 2x = -6$
$3x - 3 - 2x = -6$
$x = -3$.
(2)$\frac{x}{x + 1} + \frac{3}{x} = 1$
$x^{2} + 3(x + 1) = (x + 1)x$
$x^{2} + 3x + 3 = x^{2} + x$
$2x = -3$
$x = - \frac{3}{2}$.
经检验$x + 1 \neq 0$,$x \neq 0$,所以$x = - \frac{3}{2}$是方程的解(提醒:解分式方程不要忘了检验).
解:
(1)$3(x - 1) - 2x = -6$
$3x - 3 - 2x = -6$
$x = -3$.
(2)$\frac{x}{x + 1} + \frac{3}{x} = 1$
$x^{2} + 3(x + 1) = (x + 1)x$
$x^{2} + 3x + 3 = x^{2} + x$
$2x = -3$
$x = - \frac{3}{2}$.
经检验$x + 1 \neq 0$,$x \neq 0$,所以$x = - \frac{3}{2}$是方程的解(提醒:解分式方程不要忘了检验).
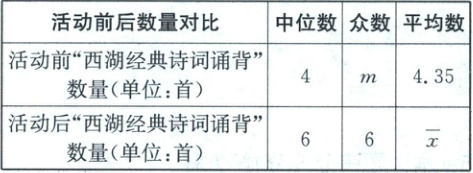
19. (本小题满分 8 分)某校组织全校 1 000 名学生进行“西湖经典诗词诵背”活动. 为了解本次活动的效果,学校团委在活动之初,随机抽取 40 名学生调查“西湖经典诗词诵背”情况,根据调查结果绘制了如下统计图:
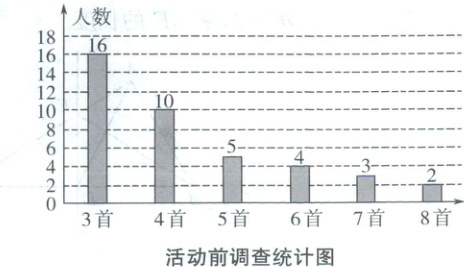
活动结束后,再次调查这 40 名学生“西湖经典诗词诵背”情况,绘制了如下统计图:
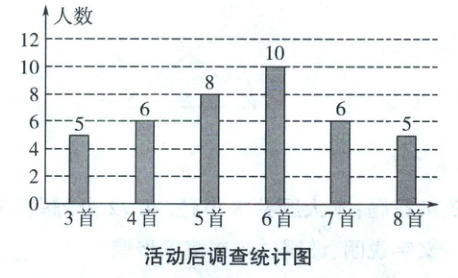
请根据调查的信息分析:
(1)估计活动结束后该校学生能诵背 7 首(含 7 首)以上的人数.
(2)$m=$
(3)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校“西湖经典诗词诵背”系列活动的效果.

活动结束后,再次调查这 40 名学生“西湖经典诗词诵背”情况,绘制了如下统计图:

请根据调查的信息分析:
(1)估计活动结束后该校学生能诵背 7 首(含 7 首)以上的人数.
(2)$m=$
3
,$\overline{x}=$5.5
.
(3)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校“西湖经典诗词诵背”系列活动的效果.
(1)$1000 × \frac{11}{40} = 275$(人).答:估计活动结束后该校有275人能诵背7首(含7首)以上.(3)活动后,从平均数分析,样本的人均诵背数量约增加了1首,众数从3到6,说明效果明显,中位数从4提升到了6,说明大部分人都在进步,活动取得了较好的效果.
答案:
19. 条形统计图+中位数+众数+平均数+用样本估计总体
解:
(1)$1000 × \frac{11}{40} = 275$(人).
答:估计活动结束后该校有275人能诵背7首(含7首)以上.
(2)3 5.5 25.
(3)活动后,从平均数分析,样本的人均诵背数量约增加了1首,众数从3到6,说明效果明显,中位数从4提升到了6,说明大部分人都在进步,活动取得了较好的效果.
解:
(1)$1000 × \frac{11}{40} = 275$(人).
答:估计活动结束后该校有275人能诵背7首(含7首)以上.
(2)3 5.5 25.
(3)活动后,从平均数分析,样本的人均诵背数量约增加了1首,众数从3到6,说明效果明显,中位数从4提升到了6,说明大部分人都在进步,活动取得了较好的效果.
查看更多完整答案,请扫码查看


