第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 下列四个图标中,属于轴对称图形的是(
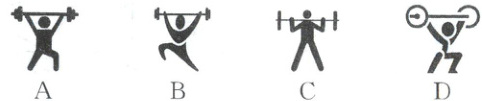
C
)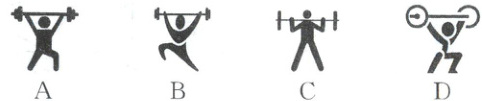
答案:
1. C [考点]轴对称图形
2. 某天14:00,我国五个城市的气温如表,其中与北京气温最接近的城市是(

A.哈尔滨
B.广州
C.武汉
D.上海
A
)
A.哈尔滨
B.广州
C.武汉
D.上海
答案:
2. A [解析]有理数的减法+实数的大小比较
∵ - 20 < - 12 < 0 < 5 < 10,且 - 12 - (- 20) = 8,0 - (- 12) = 12 > 8,
∴与北京气温最接近的城市是哈尔滨.故选A.
∵ - 20 < - 12 < 0 < 5 < 10,且 - 12 - (- 20) = 8,0 - (- 12) = 12 > 8,
∴与北京气温最接近的城市是哈尔滨.故选A.
3. 下列运算正确的是(
A.$a^{2}· a^{4}=a^{6}$
B.$(a^{2})^{3}=a^{5}$
C.$a^{6}÷ a^{2}=a^{3}$
D.$a^{4}+a^{4}=2a^{8}$
A
)A.$a^{2}· a^{4}=a^{6}$
B.$(a^{2})^{3}=a^{5}$
C.$a^{6}÷ a^{2}=a^{3}$
D.$a^{4}+a^{4}=2a^{8}$
答案:
3. A [解析]同底数幂的乘法与除法+幂的乘方+合并同类项
选项 逐项分析 正误
A a²·a⁴ = a⁶ √
B (a²)³ = a⁶ ×
C a⁶÷a² = a⁴ ×
D a⁴ + a⁴ = 2a⁴ ×
故选A.
选项 逐项分析 正误
A a²·a⁴ = a⁶ √
B (a²)³ = a⁶ ×
C a⁶÷a² = a⁴ ×
D a⁴ + a⁴ = 2a⁴ ×
故选A.
4. 如图,园林工人将绿化带上参差不齐的植物修剪平整,在此过程中绿化带上植物高度的平均数与方差均发生变化.关于这两个统计量的变化情况,描述正确的是(

A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变大
D.平均数变大,方差变小
A
)
A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变大
D.平均数变大,方差变小
答案:
4. A [解析]平均数+方差 由题知,绿化带上植物高度整体变低了,所以植物高度的平均数变小.修剪后植物高度变得比较接近,数据离散程度减小,所以方差变小.故选A.
5. 如图,$AB$,$CD$为$\odot O$的弦,$AB\perp CD$于点$E$.若$\angle BCD=54^{\circ}$,则$\angle ADC$等于(
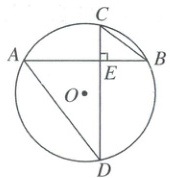
A.$27^{\circ}$
B.$36^{\circ}$
C.$46^{\circ}$
D.$54^{\circ}$
B
)
A.$27^{\circ}$
B.$36^{\circ}$
C.$46^{\circ}$
D.$54^{\circ}$
答案:
5. B [解析]圆周角定理的推论
∵AB⊥CD于点E,
∴∠BEC = 90°.
∴∠BCD + ∠ABC = 90°.
∵∠BCD = 54°,
∴∠ABC = 90° - 54° = 36°.
∴∠ADC = ∠ABC = 36°.故选B.
∵AB⊥CD于点E,
∴∠BEC = 90°.
∴∠BCD + ∠ABC = 90°.
∵∠BCD = 54°,
∴∠ABC = 90° - 54° = 36°.
∴∠ADC = ∠ABC = 36°.故选B.
6. 已知$a > b$,下列不等式中,一定成立的是(
A.$a - 1 < b - 1$
B.$a + 1 < b + 2$
C.$2a < 2b$
D.$-2a < -2b$
D
)A.$a - 1 < b - 1$
B.$a + 1 < b + 2$
C.$2a < 2b$
D.$-2a < -2b$
答案:
6. D [解析]不等式的性质 对于A,
∵a > b,
∴a - 1 > b - 1.故A错误.对于B,
∵a > b,
∴a + 1 > b + 1.但无法判断a + 1与b + 2的大小关系,故B错误.对于C,
∵a > b,
∴2a > 2b.故C错误.对于D,
∵a > b,
∴ - 2a < - 2b.故D正确.故选D.
∵a > b,
∴a - 1 > b - 1.故A错误.对于B,
∵a > b,
∴a + 1 > b + 1.但无法判断a + 1与b + 2的大小关系,故B错误.对于C,
∵a > b,
∴2a > 2b.故C错误.对于D,
∵a > b,
∴ - 2a < - 2b.故D正确.故选D.
7. 如图,在$□ ABCD$中,$AC$,$BD$为两条对角线.添加下列一个条件,仍不能判定$□ ABCD$是菱形,则这个条件是(
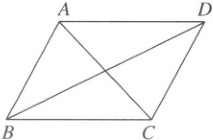
A.$AC\perp BD$
B.$AB\perp BC$
C.$AB = BC$
D.$\angle BAC = \angle DAC$
B
)
A.$AC\perp BD$
B.$AB\perp BC$
C.$AB = BC$
D.$\angle BAC = \angle DAC$
答案:
7. B [解析]菱形的判定 对于A,
∵四边形ABCD是平行四边形,AC⊥BD,
∴▱ABCD是菱形.故A不符合题意.对于B,
∵四边形ABCD是平行四边形,AB⊥BC,
∴▱ABCD是矩形.故B符合题意.对于C,
∵四边形ABCD是平行四边形,AB = BC,
∴▱ABCD是菱形.故C不符合题意.对于D,
∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DAC = ∠ACB.
∵∠BAC = ∠DAC,
∴∠BAC = ∠ACB,
∴AB = BC,
∴▱ABCD是菱形.故D不符合题意,故选B.
∵四边形ABCD是平行四边形,AC⊥BD,
∴▱ABCD是菱形.故A不符合题意.对于B,
∵四边形ABCD是平行四边形,AB⊥BC,
∴▱ABCD是矩形.故B符合题意.对于C,
∵四边形ABCD是平行四边形,AB = BC,
∴▱ABCD是菱形.故C不符合题意.对于D,
∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DAC = ∠ACB.
∵∠BAC = ∠DAC,
∴∠BAC = ∠ACB,
∴AB = BC,
∴▱ABCD是菱形.故D不符合题意,故选B.
8. 若$a + b = 5\sqrt{3}$,$ab = 12$,则$a - b$的值为(
A.$\sqrt{51}$
B.$\pm\sqrt{51}$
C.$3\sqrt{3}$
D.$\pm3\sqrt{3}$
D
)A.$\sqrt{51}$
B.$\pm\sqrt{51}$
C.$3\sqrt{3}$
D.$\pm3\sqrt{3}$
答案:
8. D [解析]完全平方公式 由题知,(a - b)² = a² + b² - 2ab = a² + b² + 2ab - 4ab = (a + b)² - 4ab = 75 - 4×12 = 27,解得a - b = ±3$\sqrt{3}$[易错:本题中a > 0,b > 0,但无法确定二者的大小关系,因此(a - b)²的平方根是一正一负,容易漏解].故选D.
9. 在2020年9月,我国提出力争在2030年前实现碳达峰,即二氧化碳排放量达到峰值并开始下降.已知某企业2024年的碳排放量为300吨,该企业为响应国家号召,提出一个减排计划:从2025年开始,每年的碳排放量均比上年减少10吨,$x$年内的碳排放量共计2450吨.为求$x$的值,列出如下方程,其中正确的是(
A.$\frac{1}{2}x(580 - 10x) = 2450$
B.$\frac{1}{2}x(590 - 10x) = 2450$
C.$\frac{1}{2}(x - 1)(590 - 10x) = 2450$
D.$\frac{1}{2}x(600 - 10x) = 2450$
B
)A.$\frac{1}{2}x(580 - 10x) = 2450$
B.$\frac{1}{2}x(590 - 10x) = 2450$
C.$\frac{1}{2}(x - 1)(590 - 10x) = 2450$
D.$\frac{1}{2}x(600 - 10x) = 2450$
答案:
9. B [解析]由实际问题抽象出一元二次方程 由题知,2025年的碳排放量为300 - 10 = 290(吨),第x年的碳排放量为290 - 10(x - 1) = (300 - 10x)(吨),所以x年内碳排放量的总和为$\frac{x(290 + 300 - 10x)}{2}$ = 2450[技巧:求和公式:1 + 2 + 3 +... + n = $\frac{n(1 + n)}{2}$],即$\frac{1}{2}$x(590 - 10x) = 2450.故选B.
知识拓展
常见的求和公式
(1)1 + 2 + 3 + … + n = $\frac{n(1 + n)}{2}$;
(2)1 + 3 + 5 + … + (2n - 1) = n²;
(3)1² + 2² + 3² + … + n² = $\frac{n(n + 1)(2n + 1)}{6}$;
(4)1³ + 2³ + 3³ + … + n³ = [$\frac{n(n + 1)}{2}$]²;
(5)1×2 + 2×3 + 3×4 +... + n(n + 1) = $\frac{n(n + 1)(n + 2)}{3}$;
(6)$\frac{1}{1×2}$ + $\frac{1}{2×3}$ + $\frac{1}{3×4}$ + … + $\frac{1}{n(n + 1)}$ = $\frac{n}{n + 1}$.
知识拓展
常见的求和公式
(1)1 + 2 + 3 + … + n = $\frac{n(1 + n)}{2}$;
(2)1 + 3 + 5 + … + (2n - 1) = n²;
(3)1² + 2² + 3² + … + n² = $\frac{n(n + 1)(2n + 1)}{6}$;
(4)1³ + 2³ + 3³ + … + n³ = [$\frac{n(n + 1)}{2}$]²;
(5)1×2 + 2×3 + 3×4 +... + n(n + 1) = $\frac{n(n + 1)(n + 2)}{3}$;
(6)$\frac{1}{1×2}$ + $\frac{1}{2×3}$ + $\frac{1}{3×4}$ + … + $\frac{1}{n(n + 1)}$ = $\frac{n}{n + 1}$.
查看更多完整答案,请扫码查看


