第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 工厂检测四个零件的质量(单位:克),超过标准质量的克数记为正数,不足标准质量的克数记为负数,其中最接近标准质量的是(
A.$ +1.3 $
B.$ -2.1 $
C.$ +0.1 $
D.$ -0.8 $
C
)A.$ +1.3 $
B.$ -2.1 $
C.$ +0.1 $
D.$ -0.8 $
答案:
1.C 【考点】正负数的意义+绝对值
2. 人工智能模型的参数量越大,理解能力越强. Deepseek V3-0324模型参数可达685 000 000 000个,其中数685 000 000 000用科学记数法表示为(
A.$ 6.85×10^{11} $
B.$ 6.85×10^{10} $
C.$ 68.5×10^{11} $
D.$ 68.5×10^{10} $
A
)A.$ 6.85×10^{11} $
B.$ 6.85×10^{10} $
C.$ 68.5×10^{11} $
D.$ 68.5×10^{10} $
答案:
2.A 【考点】科学记数法
3. 一个不透明的袋子里装有1个红球和3个白球,它们除颜色外均相同. 从袋中任意摸出一个球是红球的概率为(
A.$ \frac{3}{4} $
B.$ \frac{2}{3} $
C.$ \frac{1}{3} $
D.$ \frac{1}{4} $
D
)A.$ \frac{3}{4} $
B.$ \frac{2}{3} $
C.$ \frac{1}{3} $
D.$ \frac{1}{4} $
答案:
3.D 【解析】概率公式 由题知,从袋中任意摸出一个球是红球的概率为$\frac{1}{1+3}=\frac{1}{4}$.故选D.
4. 某几何体的三视图如图所示,则该几何体是(
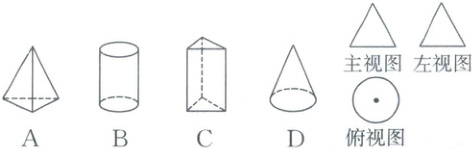
D
)
答案:
4.D 【考点】由三视图还原几何体
5. 下列运算结果正确的是( )
A.$ 2a^{3}+a^{3}=3a^{6} $
B.$ 2a^{3}·a^{3}=2a^{6} $
C.$ (2a^{3})^{3}=6a^{9} $
D.$ 2a^{3}÷a=a^{2} $
A.$ 2a^{3}+a^{3}=3a^{6} $
B.$ 2a^{3}·a^{3}=2a^{6} $
C.$ (2a^{3})^{3}=6a^{9} $
D.$ 2a^{3}÷a=a^{2} $
答案:
5.B 【解析】合并同类项+同底数幂的乘、除法+积的乘方
|选项|逐项分析|正误|
|----|----|----|
|A|$2a^{3}+a^{3}=3a^{3}$|×|
|B|$2a^{3}· a^{3}=2a^{6}$|√|
|C|$(2a^{3})^{3}=2^{3}· a^{9}=8a^{9}$|×|
|D|$2a^{3}÷ a=2a^{2}$|×|
故选B.
|选项|逐项分析|正误|
|----|----|----|
|A|$2a^{3}+a^{3}=3a^{3}$|×|
|B|$2a^{3}· a^{3}=2a^{6}$|√|
|C|$(2a^{3})^{3}=2^{3}· a^{9}=8a^{9}$|×|
|D|$2a^{3}÷ a=2a^{2}$|×|
故选B.
6. 如图,在平面直角坐标系中,已知点$ A(0,2) $,$ B(4,2) $,线段AB向上平移后,A,B的对应点分别为$ A' $,$ B' $,若四边形$ ABB'A' $是正方形,则点$ A' $的坐标为(
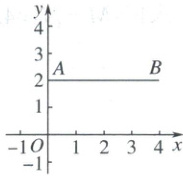
A.$ (0,4) $
B.$ (0,6) $
C.$ (0,-2) $
D.$ (0,-4) $
B
)
A.$ (0,4) $
B.$ (0,6) $
C.$ (0,-2) $
D.$ (0,-4) $
答案:
6.B 【解析】正方形的性质+平移的性质
∵点$A(0,2)$,$B(4,2)$,
∴$AB = 4$.
∵将线段$AB$向上平移后,得到四边形$ABB'A'$是正方形,
∴$AA' = 4$,点$A'$在$y$轴上.
∴$OA' = AA' + OA = 4 + 2 = 6$.
∴点$A'$的坐标为$(0,6)$.故选B.
∵点$A(0,2)$,$B(4,2)$,
∴$AB = 4$.
∵将线段$AB$向上平移后,得到四边形$ABB'A'$是正方形,
∴$AA' = 4$,点$A'$在$y$轴上.
∴$OA' = AA' + OA = 4 + 2 = 6$.
∴点$A'$的坐标为$(0,6)$.故选B.
7. 某企业生产一批工艺品,为了尽快完成任务,实际每天生产工艺品比原计划多200个. 已知实际生产3 000个工艺品与原计划生产1 800个所用的时间相同,若设原计划每天生产$ x $个工艺品,则可列方程为(
A.$ \frac{1\ 800}{x - 200}=\frac{3\ 000}{x} $
B.$ \frac{1\ 800}{x + 200}=\frac{3\ 000}{x} $
C.$ \frac{1\ 800}{x}=\frac{3\ 000}{x + 200} $
D.$ \frac{1\ 800}{x}=\frac{3\ 000}{x - 200} $
C
)A.$ \frac{1\ 800}{x - 200}=\frac{3\ 000}{x} $
B.$ \frac{1\ 800}{x + 200}=\frac{3\ 000}{x} $
C.$ \frac{1\ 800}{x}=\frac{3\ 000}{x + 200} $
D.$ \frac{1\ 800}{x}=\frac{3\ 000}{x - 200} $
答案:
7.C 【考点】由实际问题抽象出分式方程
8. 如图,$ △ABC $内接于$ ⊙O $,CE是$ ⊙O $的切线,连接CO并延长交弦AB于点D. 若$ \overset{\frown}{BC} $所对圆心角为$ 80^{\circ} $,$ ∠ACE = α(0^{\circ} < α < 90^{\circ}) $,则$ ∠CDB $的度数为( )
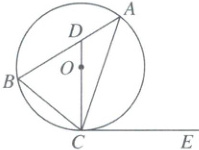
A.$ 130^{\circ}-α $
B.$ 170^{\circ}-α $
C.$ 80^{\circ}+α $
D.$ 40^{\circ}+α $

A.$ 130^{\circ}-α $
B.$ 170^{\circ}-α $
C.$ 80^{\circ}+α $
D.$ 40^{\circ}+α $
答案:
8.A 【解析】圆周角定理+切线的性质+三角形外角的性质 如图,连接$OB$(巧作辅助线:构造圆心角,从而得到圆心角与圆周角的关系).
∵$\overset{\frown}{BC}$所对圆心角为$80^{\circ}$,
∴$\angle BOC = 80^{\circ}$.
∴$\angle A = \frac{1}{2}\angle BOC = 40^{\circ}$.
∵$CE$是$\odot O$的切线,
∴$\angle OCE = 90^{\circ}$.
∵$\angle ACE = \alpha$,
∴$\angle ACD = \angle OCE - \angle ACE = 90^{\circ} - \alpha$.

∴$\angle CDB = \angle A + \angle ACD = 40^{\circ} + 90^{\circ} - \alpha = 130^{\circ} - \alpha$.故选A.
8.A 【解析】圆周角定理+切线的性质+三角形外角的性质 如图,连接$OB$(巧作辅助线:构造圆心角,从而得到圆心角与圆周角的关系).
∵$\overset{\frown}{BC}$所对圆心角为$80^{\circ}$,
∴$\angle BOC = 80^{\circ}$.
∴$\angle A = \frac{1}{2}\angle BOC = 40^{\circ}$.
∵$CE$是$\odot O$的切线,
∴$\angle OCE = 90^{\circ}$.
∵$\angle ACE = \alpha$,
∴$\angle ACD = \angle OCE - \angle ACE = 90^{\circ} - \alpha$.

∴$\angle CDB = \angle A + \angle ACD = 40^{\circ} + 90^{\circ} - \alpha = 130^{\circ} - \alpha$.故选A.
9. 如图,在$ △ABC $中,$ ∠A = 60^{\circ} $,点D,E,F分别在边BC,AB,AC上,点B,D关于EG对称,点C,D关于FH对称. 若要求出$ △DEF $的周长,只需知道( )
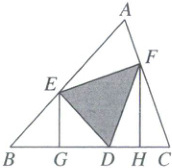
A.AE和AF的长
B.BE和CF的长
C.EG和FH的长
D.BG和CH的长

A.AE和AF的长
B.BE和CF的长
C.EG和FH的长
D.BG和CH的长
答案:
9.B 【解析】轴对称的性质+三角形内角和定理+勾股定理
∵点$B$,$D$关于$EG$对称,点$C$,$D$关于$FH$对称,
∴$DE = BE$,$DF = CF$,$\angle B = \angle BDE$,$\angle C = \angle CDF$.
∴$\angle BDE + \angle CDF = \angle B + \angle C$.
∵$\angle A = 60^{\circ}$,
∴$\angle BDE + \angle CDF = \angle B + \angle C = 180^{\circ} - \angle A = 120^{\circ}$.
∴$\angle EDF = 180^{\circ} - (\angle BDE + \angle CDF) = 60^{\circ}$.设$DE = BE = 2a$,$DF = CF = b$,如图,过点$E$作$EP \perp DF$于点$P$(巧作辅助线:构造直角三角形,求$EF$),则$\angle DEP = 30^{\circ}$.
∴$DP = \frac{1}{2}DE = a$.
∴$PE = \sqrt{DE^{2} - DP^{2}} = \sqrt{3}a$,$PF = b - a$.
∴$EF = \sqrt{PE^{2} + PF^{2}} = \sqrt{4a^{2} - 2ab + b^{2}}$.
∴$\triangle DEF$的周长为$DE + DF + EF = 2a + b + \sqrt{4a^{2} - 2ab + b^{2}}$.
∴$\triangle DEF$的周长只与$BE$,$CF$的长有关.故选B.

9.B 【解析】轴对称的性质+三角形内角和定理+勾股定理
∵点$B$,$D$关于$EG$对称,点$C$,$D$关于$FH$对称,
∴$DE = BE$,$DF = CF$,$\angle B = \angle BDE$,$\angle C = \angle CDF$.
∴$\angle BDE + \angle CDF = \angle B + \angle C$.
∵$\angle A = 60^{\circ}$,
∴$\angle BDE + \angle CDF = \angle B + \angle C = 180^{\circ} - \angle A = 120^{\circ}$.
∴$\angle EDF = 180^{\circ} - (\angle BDE + \angle CDF) = 60^{\circ}$.设$DE = BE = 2a$,$DF = CF = b$,如图,过点$E$作$EP \perp DF$于点$P$(巧作辅助线:构造直角三角形,求$EF$),则$\angle DEP = 30^{\circ}$.
∴$DP = \frac{1}{2}DE = a$.
∴$PE = \sqrt{DE^{2} - DP^{2}} = \sqrt{3}a$,$PF = b - a$.
∴$EF = \sqrt{PE^{2} + PF^{2}} = \sqrt{4a^{2} - 2ab + b^{2}}$.
∴$\triangle DEF$的周长为$DE + DF + EF = 2a + b + \sqrt{4a^{2} - 2ab + b^{2}}$.
∴$\triangle DEF$的周长只与$BE$,$CF$的长有关.故选B.

查看更多完整答案,请扫码查看


