第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
20. (本小题满分8分)某校举办手工创意比赛,有30名学生报名参加. 参赛作品的评分项目包括创意、技巧和完成度,并依次按$ 5:3:2 $比例计算总评成绩. 各项目得分为六位评委评分的平均数. 如表是小聪、小慧的项目得分和总评成绩表,其中六位评委给小慧打出的创意项目分数如下(单位:分):89,88,86,87,84,82. 如图是30名学生的总评成绩频数直方图(每组含前一个边界值,不含后一个边界值).
小聪、小慧的项目得分和总评成绩表(单位:分)
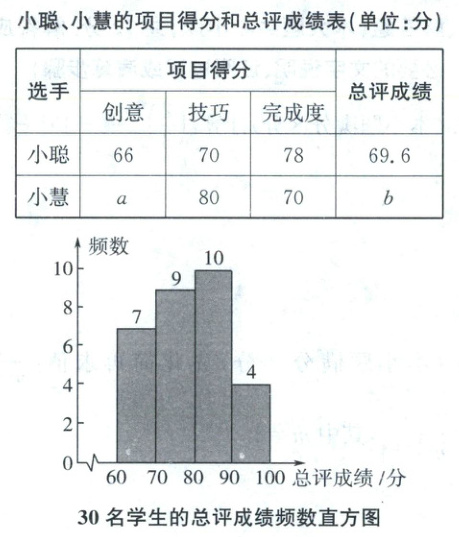
(1) 求$ a $,$ b $的值.
(2) 学校根据总评成绩选出前15名评为校园手工达人,判断小聪、小慧能否入选,并说明理由.
小聪、小慧的项目得分和总评成绩表(单位:分)

(1) 求$ a $,$ b $的值.
(2) 学校根据总评成绩选出前15名评为校园手工达人,判断小聪、小慧能否入选,并说明理由.
答案:
20.频数分布直方图+加权平均数+中位数
解:
(1)$a = \frac{89 + 88 + 86 + 87 + 84 + 82}{6} = 86$, (2分)
$b = 86 × 0.5 + 80 × 0.3 + 70 × 0.2 = 81$. (4分)
(2)
∵前$15$名的总评成绩大于等于总评成绩的中位数,中位数落在$70 \sim 80$之间,而小聪的总评成绩$69.6 < 70$,
∴小聪不能入选,小慧的总评成绩$81 > 80$,
∴小慧能入选. (8分)
(言之有理即可)
解:
(1)$a = \frac{89 + 88 + 86 + 87 + 84 + 82}{6} = 86$, (2分)
$b = 86 × 0.5 + 80 × 0.3 + 70 × 0.2 = 81$. (4分)
(2)
∵前$15$名的总评成绩大于等于总评成绩的中位数,中位数落在$70 \sim 80$之间,而小聪的总评成绩$69.6 < 70$,
∴小聪不能入选,小慧的总评成绩$81 > 80$,
∴小慧能入选. (8分)
(言之有理即可)
21. (本小题满分8分)如图,$ △ABC $内接于$ ⊙O $($ AC < BC $),直径$ AB = 4 $,点P在$ \overset{\frown}{BC} $上.
(1) 请用无刻度的直尺和圆规在$ ⊙O $上找一点D,使得$ ∠CPD = 2∠B $.
(2) 在(1)的条件下,连接CD,已知$ CD = 3 $,为了求$ \sin∠CPD $,小明和小丽提出了各自的研究思路. 请选择一种研究思路,求$ \sin∠CPD $.

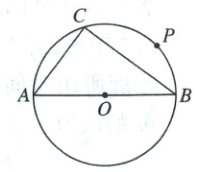
(1) 请用无刻度的直尺和圆规在$ ⊙O $上找一点D,使得$ ∠CPD = 2∠B $.
(2) 在(1)的条件下,连接CD,已知$ CD = 3 $,为了求$ \sin∠CPD $,小明和小丽提出了各自的研究思路. 请选择一种研究思路,求$ \sin∠CPD $.


答案:
21.尺规作图+圆周角定理及其推论+垂径定理+解直角三角形
解:
(1)如图1,点$D$为所求作(点拨:以$A$为圆心,$AC$为半径画弧,交$\odot O$于点$D$). (4分)

(其他画法酌情给分)
(2)选择小明的研究思路,如图2,

∵$DF$是直径(关键:作直径$DF$构造直径所对的圆周角),
∴$\angle FCD = 90^{\circ}$.
∴在$Rt \triangle CDF$中,$\sin \angle CFD = \frac{CD}{DF} = \frac{3}{4}$.
∴$\sin \angle CPD = \sin \angle CFD = \frac{3}{4}$. (8分)
选择小丽的研究思路,如图3,

由
(1)可得$\overset{\frown}{AC} = \overset{\frown}{AD}$,
∴$CE \perp AB$,$CE = \frac{1}{2}CD = \frac{3}{2}$(提示:垂径定理).
∴在$Rt \triangle COE$中,$\sin \angle COE = \frac{CE}{CO} = \frac{\frac{3}{2}}{\frac{1}{2}AB} = \frac{3}{4}$.
∵$CO = BO$,
∴$\angle COE = 2 \angle CBA = \angle CPD$.
∴$\sin \angle CPD = \sin \angle COE = \frac{3}{4}$. (8分)
21.尺规作图+圆周角定理及其推论+垂径定理+解直角三角形
解:
(1)如图1,点$D$为所求作(点拨:以$A$为圆心,$AC$为半径画弧,交$\odot O$于点$D$). (4分)

(其他画法酌情给分)
(2)选择小明的研究思路,如图2,

∵$DF$是直径(关键:作直径$DF$构造直径所对的圆周角),
∴$\angle FCD = 90^{\circ}$.
∴在$Rt \triangle CDF$中,$\sin \angle CFD = \frac{CD}{DF} = \frac{3}{4}$.
∴$\sin \angle CPD = \sin \angle CFD = \frac{3}{4}$. (8分)
选择小丽的研究思路,如图3,

由
(1)可得$\overset{\frown}{AC} = \overset{\frown}{AD}$,
∴$CE \perp AB$,$CE = \frac{1}{2}CD = \frac{3}{2}$(提示:垂径定理).
∴在$Rt \triangle COE$中,$\sin \angle COE = \frac{CE}{CO} = \frac{\frac{3}{2}}{\frac{1}{2}AB} = \frac{3}{4}$.
∵$CO = BO$,
∴$\angle COE = 2 \angle CBA = \angle CPD$.
∴$\sin \angle CPD = \sin \angle COE = \frac{3}{4}$. (8分)
22. (本小题满分10分)数学应用:小光骑着某款变速自行车先沿平路,再沿斜坡向上骑行.
素材一 如图,该款自行车前链轮齿数为40齿,后链轮齿数可设定在11齿~42齿之间(包含边界值),齿轮比$ = \frac{前链轮齿数}{后链轮齿数} $.
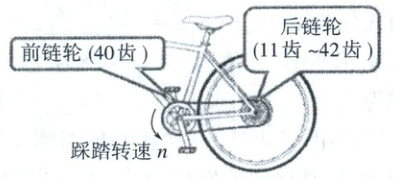
素材二 记车速为$ v $(米/秒)、踩踏转速为$ n $(转/分钟)、齿轮比为$ i $,已知$ v $,$ n $,$ i $满足$ v = \frac{ni}{25} $.
素材三 小光平路骑行时后链轮齿数为24齿,车速$ v $为6米/秒.
(1) 求小光平路骑行时的踩踏转速$ n $.
(2) 小光在上坡的骑行车速与在平路一样,上坡的踩踏转速比平路减少了15~30转/分钟(包含边界值),求上坡的后链轮齿数的设定范围.
素材一 如图,该款自行车前链轮齿数为40齿,后链轮齿数可设定在11齿~42齿之间(包含边界值),齿轮比$ = \frac{前链轮齿数}{后链轮齿数} $.

素材二 记车速为$ v $(米/秒)、踩踏转速为$ n $(转/分钟)、齿轮比为$ i $,已知$ v $,$ n $,$ i $满足$ v = \frac{ni}{25} $.
素材三 小光平路骑行时后链轮齿数为24齿,车速$ v $为6米/秒.
(1) 求小光平路骑行时的踩踏转速$ n $.
(2) 小光在上坡的骑行车速与在平路一样,上坡的踩踏转速比平路减少了15~30转/分钟(包含边界值),求上坡的后链轮齿数的设定范围.
答案:
22.一次函数的应用+一元一次方程的应用
解:
(1)
∵前链轮齿数为$40$齿,后链轮齿数为$24$齿,
∴$i = \frac{40}{24} = \frac{5}{3}$(难点:将实际问题转化为数学问题,理解公式中字母的意义). (1分)
将$v = 6$,$i = \frac{5}{3}$代入$v = \frac{ni}{25}$,得$6 = \frac{5n}{3 × 25}$.
解得$n = 90$.
答:小光平路骑行时的踩踏转速为$90$转/分钟. (4分)
(2)设后链轮齿数为$x$齿,
将$v = 6$,$i = \frac{40}{x}$代入$v = \frac{ni}{25}$,得$6 = \frac{8n}{5x}$,
∴$x = \frac{4n}{15}$.
∵上坡的踩踏转速$n$降低$15 \sim 30$转/分钟(包含边界值),
∴$60 \leq n \leq 75$(关键:由转速范围,转化到齿数的设定范围).
∵当$n = 60$时,$x = 16$,当$n = 75$时,$x = 20$,
且$\frac{4}{15} > 0$,
∴当$60 \leq n \leq 75$时,$x$随$n$的增大而增大.
∴$16 \leq x \leq 20$.
答:后链轮齿数的设定范围为$16 \sim 20$(包含边界值). (10分)
解:
(1)
∵前链轮齿数为$40$齿,后链轮齿数为$24$齿,
∴$i = \frac{40}{24} = \frac{5}{3}$(难点:将实际问题转化为数学问题,理解公式中字母的意义). (1分)
将$v = 6$,$i = \frac{5}{3}$代入$v = \frac{ni}{25}$,得$6 = \frac{5n}{3 × 25}$.
解得$n = 90$.
答:小光平路骑行时的踩踏转速为$90$转/分钟. (4分)
(2)设后链轮齿数为$x$齿,
将$v = 6$,$i = \frac{40}{x}$代入$v = \frac{ni}{25}$,得$6 = \frac{8n}{5x}$,
∴$x = \frac{4n}{15}$.
∵上坡的踩踏转速$n$降低$15 \sim 30$转/分钟(包含边界值),
∴$60 \leq n \leq 75$(关键:由转速范围,转化到齿数的设定范围).
∵当$n = 60$时,$x = 16$,当$n = 75$时,$x = 20$,
且$\frac{4}{15} > 0$,
∴当$60 \leq n \leq 75$时,$x$随$n$的增大而增大.
∴$16 \leq x \leq 20$.
答:后链轮齿数的设定范围为$16 \sim 20$(包含边界值). (10分)
查看更多完整答案,请扫码查看


