第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
20. (本小题满分8分)为了解某校七年级学生每周课外阅读的时间(单位:小时),随机抽查了该校七年级50名学生上周课外阅读的时间,统计结果如图、表所示.
被抽查学生的阅读时间分布表
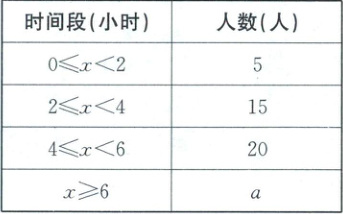
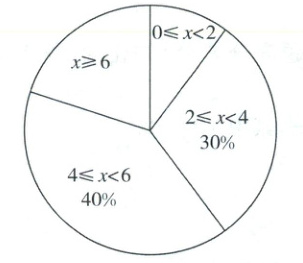
被抽查学生的阅读时间统计图
请根据相关信息,解答下列问题:
(1)计算表中 $ a $ 的值以及图中“$ x \geq 6 $”时间段对应的扇形圆心角度数.
(2)求样本数据的中位数所在的时间段.
(3)根据样本数据,估计该校七年级800名学生每周课外阅读不低于4小时的人数.
被抽查学生的阅读时间分布表


被抽查学生的阅读时间统计图
请根据相关信息,解答下列问题:
(1)计算表中 $ a $ 的值以及图中“$ x \geq 6 $”时间段对应的扇形圆心角度数.
(2)求样本数据的中位数所在的时间段.
(3)根据样本数据,估计该校七年级800名学生每周课外阅读不低于4小时的人数.
答案:
20. 扇形统计图 + 中位数 + 用样本估计总体 + 频数分布表
解:
(1)$a = 50 - 5 - 15 - 20 = 10$。
题图中“$x\geq6$”时间段对应的扇形圆心角度数为$\frac{10}{50}×360°=72°$。
(2)由被抽查学生的阅读时间分布表可知,在50个数据中第25个数据和第26个数据都在“$4\leq x<6$”时间段,所以样本数据的中位数所在的时间段为“$4\leq x<6$”。
(3)$\frac{20 + 10}{50}×800 = 480$(人)。
答:估计该校七年级800名学生每周课外阅读不低于4小时的有480人。
解:
(1)$a = 50 - 5 - 15 - 20 = 10$。
题图中“$x\geq6$”时间段对应的扇形圆心角度数为$\frac{10}{50}×360°=72°$。
(2)由被抽查学生的阅读时间分布表可知,在50个数据中第25个数据和第26个数据都在“$4\leq x<6$”时间段,所以样本数据的中位数所在的时间段为“$4\leq x<6$”。
(3)$\frac{20 + 10}{50}×800 = 480$(人)。
答:估计该校七年级800名学生每周课外阅读不低于4小时的有480人。
21. (本小题满分8分)【问题提出】如图,折叠矩形纸片 $ ABCD $,使得点 $ B $ 与点 $ A $ 重合,则折痕与边 $ AB $,$ CD $ 的交点 $ E $,$ F $ 将这组对边两等分. 如何将矩形纸片的边三等分呢?
【问题思考】如图,将矩形纸片分别沿 $ AC $,$ BF $ 折叠后展平,折痕交于点 $ P $.
(1)求证:$ CP = \frac{1}{3}CA $.
(2)请过点 $ P $ 折叠,在 $ CD $ 上找到一点 $ G $,使 $ CG = \frac{1}{3}CD $(要求:在图中画出折痕).
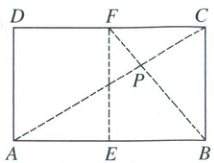
【问题思考】如图,将矩形纸片分别沿 $ AC $,$ BF $ 折叠后展平,折痕交于点 $ P $.
(1)求证:$ CP = \frac{1}{3}CA $.
(2)请过点 $ P $ 折叠,在 $ CD $ 上找到一点 $ G $,使 $ CG = \frac{1}{3}CD $(要求:在图中画出折痕).

答案:
21. 矩形的性质 + 相似三角形的判定与性质
解:
(1)证明:$\because$四边形ABCD为矩形,$\therefore AB// CD$,$AB = CD$。
由题意得F为CD的中点,可知$CF=\frac{1}{2}CD$,
则$CF=\frac{1}{2}AB$。
由$AB// CD$得,$\triangle PCF\sim \triangle PAB$,
$\therefore \frac{CP}{AP}=\frac{CF}{AB}=\frac{1}{2}$。
所以$CP=\frac{1}{3}AC$。
(2)如图,折痕正确并标注点G。

【解题过程】过点P作$GH// AD$分别交CD,AB于点G,H。
则四边形AHGD为矩形,$\therefore AH = DG$。
$\because CG// AH$,
$\therefore \triangle CGP\sim \triangle AHP$。
$\because \frac{CG}{AH}=\frac{CP}{AP}=\frac{1}{2}$。
$\therefore AH = 2CG$。
$\therefore DG = 2CG$。
$\therefore CG=\frac{1}{3}CD$。
21. 矩形的性质 + 相似三角形的判定与性质
解:
(1)证明:$\because$四边形ABCD为矩形,$\therefore AB// CD$,$AB = CD$。
由题意得F为CD的中点,可知$CF=\frac{1}{2}CD$,
则$CF=\frac{1}{2}AB$。
由$AB// CD$得,$\triangle PCF\sim \triangle PAB$,
$\therefore \frac{CP}{AP}=\frac{CF}{AB}=\frac{1}{2}$。
所以$CP=\frac{1}{3}AC$。
(2)如图,折痕正确并标注点G。

【解题过程】过点P作$GH// AD$分别交CD,AB于点G,H。
则四边形AHGD为矩形,$\therefore AH = DG$。
$\because CG// AH$,
$\therefore \triangle CGP\sim \triangle AHP$。
$\because \frac{CG}{AH}=\frac{CP}{AP}=\frac{1}{2}$。
$\therefore AH = 2CG$。
$\therefore DG = 2CG$。
$\therefore CG=\frac{1}{3}CD$。
22. (本小题满分10分)2024年“有礼杯”衢州马拉松于11月24日开跑,小明和小聪一起报名参加了“迷你跑”的比赛. 小明以一定的速度跑到3000米处的补给点休息了一段时间后,继续以原速前行,在距离终点500米处因体力不支,最终以100米/分的速度坚持跑到终点;小聪在途中休息了5分钟后,以原来的 $ \frac{4}{3} $ 倍的速度冲向终点. 如图是小明和小聪在比赛过程中所跑的路程 $ s $(米)和跑步时间 $ t $(分)的函数关系图. 根据图象回答下列问题:
(1)求 $ a $ 的值.
(2)求图中线段 $ BC $ 对应的函数表达式.
(3)求小聪休息前的速度.
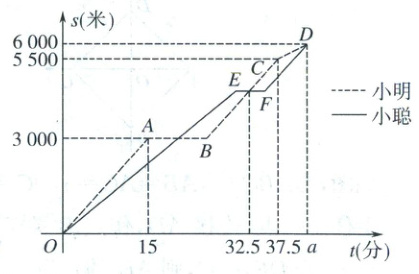
(1)求 $ a $ 的值.
(2)求图中线段 $ BC $ 对应的函数表达式.
(3)求小聪休息前的速度.

答案:
22. 一次函数的实际应用 + 分式方程的实际应用
解:
(1)$a = 37.5 + 500÷100 = 42.5$。
(2)解法一:由题意得,小明中途休息的时长为$37.5 - 5500÷(3000÷15)=10$(分),
所以点B的坐标为$(25,3000)$,
又点C的坐标为$(37.5,5500)$,
设线段BC对应的函数表达式为$s = kt + b$,
则$\begin{cases}25k + b = 3000\\37.5k + b = 5500\end{cases}$解得$\begin{cases}k = 200\\b = - 2000\end{cases}$
所以线段BC对应的函数表达式为$s = 200t - 2000(25\leq t\leq37.5)$。
解法二:由题意得,当$0<t\leq15$时,$v_{小明}=3000÷15 = 200$(米/分)(提示:速度 = 路程÷时间)。
设线段BC对应的函数表达式为$s = 200t + b$,把点C的坐标$(37.5,5500)$代入,得$5500 = 200×37.5 + b$,解得$b = - 2000$。
所以$s = 200t - 2000$。
又因为当$s = 3000$时,$t = 25$。
所以线段BC对应的函数表达式为$s = 200t - 2000(25\leq t\leq37.5)$。
(3)结合题图及
(2)可知,当$t = 32.5$时,$s = 4500$。
设小聪休息前的速度为$v$米/分,
则$\frac{4500}{v}+\frac{6000 - 4500}{\frac{4}{3}v}+5 = 42.5$。
解得$v = 150$。
经检验,$v = 150$是原方程的解,且符合题意。
答:小聪休息前的速度为150米/分。
解:
(1)$a = 37.5 + 500÷100 = 42.5$。
(2)解法一:由题意得,小明中途休息的时长为$37.5 - 5500÷(3000÷15)=10$(分),
所以点B的坐标为$(25,3000)$,
又点C的坐标为$(37.5,5500)$,
设线段BC对应的函数表达式为$s = kt + b$,
则$\begin{cases}25k + b = 3000\\37.5k + b = 5500\end{cases}$解得$\begin{cases}k = 200\\b = - 2000\end{cases}$
所以线段BC对应的函数表达式为$s = 200t - 2000(25\leq t\leq37.5)$。
解法二:由题意得,当$0<t\leq15$时,$v_{小明}=3000÷15 = 200$(米/分)(提示:速度 = 路程÷时间)。
设线段BC对应的函数表达式为$s = 200t + b$,把点C的坐标$(37.5,5500)$代入,得$5500 = 200×37.5 + b$,解得$b = - 2000$。
所以$s = 200t - 2000$。
又因为当$s = 3000$时,$t = 25$。
所以线段BC对应的函数表达式为$s = 200t - 2000(25\leq t\leq37.5)$。
(3)结合题图及
(2)可知,当$t = 32.5$时,$s = 4500$。
设小聪休息前的速度为$v$米/分,
则$\frac{4500}{v}+\frac{6000 - 4500}{\frac{4}{3}v}+5 = 42.5$。
解得$v = 150$。
经检验,$v = 150$是原方程的解,且符合题意。
答:小聪休息前的速度为150米/分。
查看更多完整答案,请扫码查看


