第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
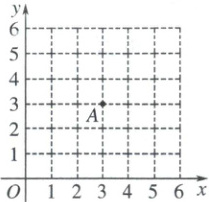
9. 如图,在“探索一次函数$y = kx + b$中$k$,$b$与图象的关系”活动中,已知点$A(3,3)$,点$P(m,n)$在第一象限内,若一次函数$y = kx + b$图象经过$A$,$P$,则下列判断正确的是( )
A.当$m > n$时,$b > 0$
B.当$m < n$时,$b < 0$
C.当$m + n = 3$时,$k > 0$
D.当$m + n = 3$时,$k < 0$

A.当$m > n$时,$b > 0$
B.当$m < n$时,$b < 0$
C.当$m + n = 3$时,$k > 0$
D.当$m + n = 3$时,$k < 0$
答案:
9 C 【解析】一次函数的图象与性质 如图,当点$P$为$(2,1)$时,满足$m > n$,但$b < 0$(方法:取特殊值,画出图象,根据图象判断),故A错误. 当点$P$为$(1,4)$时,满足$m < n$,但$b > 0$,故B错误. 当$m + n = 3$时,由题意可知$0 < m < 3$,$0 < n < 3$,又$\because$一次函数$y = kx + b$的图象经过点$A(3,3)$,$P(m,n)$,$\therefore y$随$x$的增大而增大. $\therefore k > 0$. 故C正确,D错误. 故选C.

9 C 【解析】一次函数的图象与性质 如图,当点$P$为$(2,1)$时,满足$m > n$,但$b < 0$(方法:取特殊值,画出图象,根据图象判断),故A错误. 当点$P$为$(1,4)$时,满足$m < n$,但$b > 0$,故B错误. 当$m + n = 3$时,由题意可知$0 < m < 3$,$0 < n < 3$,又$\because$一次函数$y = kx + b$的图象经过点$A(3,3)$,$P(m,n)$,$\therefore y$随$x$的增大而增大. $\therefore k > 0$. 故C正确,D错误. 故选C.

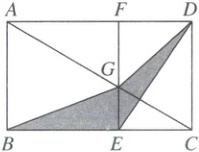
10. 如图,在矩形$ABCD$中,$E$是$BC$上一点,$BE = AB$,$EF\perp BC$交$AD$于点$F$,交对角线$AC$于点$G$,连接$BG$,$DG$,$DE$. 若求阴影部分的面积,则只需要知道( )
A.$\triangle ADG$的面积
B.$\triangle ABC$的面积
C.四边形$ABEF$的面积
D.四边形$CDFE$的面积

A.$\triangle ADG$的面积
B.$\triangle ABC$的面积
C.四边形$ABEF$的面积
D.四边形$CDFE$的面积
答案:
10 D 【解析】矩形的性质+正方形的判定与性质+三角形的面积公式+相似三角形的判定与性质
[第1步,证明四边形$ABEF$是正方形]
$\because$四边形$ABCD$是矩形,$\therefore \angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ}$. $\because EF \perp BC$,$\therefore \angle BEF = \angle CEF = 90^{\circ}$. $\therefore$四边形$ABEF$和四边形$CDFE$都是矩形(关键:根据已知条件判定特殊四边形). 又$\because BE = AB$,$\therefore$四边形$ABEF$是正方形.
[第2步,证明$\triangle AGF \sim \triangle CGE$,表示出$GE$的长]
设$BE = EF = AF = a$,$CE = b$,$GE = x$(方法:根据线段长度不同设未知参数,结合图形特征建立等量关系式),$\therefore GF = EF - GE = a - x$. $\because AD // BC$,$\therefore \triangle AGF \sim \triangle CGE$. $\therefore \frac{AF}{CE} = \frac{GF}{GE}$,即$\frac{a}{b} = \frac{a - x}{x}$,$\therefore x = \frac{ab}{a + b}$(重点:当等式中出现三个未知参数,且存在等量关系时,常采用消元法,即利用等式的性质消去某一个未知数).
[第3步,利用分割法求阴影部分的面积,结合矩形$CDFE$的面积可得$S_{阴影} = \frac{1}{2} S_{矩形CDFE}$]
$\therefore S_{\triangle BEG} = \frac{1}{2} BE · GE = \frac{1}{2} ax$,$S_{\triangle DEG} = \frac{1}{2} GE · EC = \frac{1}{2} bx$.
$\therefore S_{阴影} = S_{\triangle BEG} + S_{\triangle DEG} = \frac{1}{2} x(a + b) = \frac{1}{2} ab$. 又$\because S_{矩形CDFE} = ab$,$\therefore S_{阴影} = \frac{1}{2} S_{矩形CDFE}$. $\therefore$若求阴影部分的面积,则只需要知道四边形$CDFE$的面积. 故选D.
知识拓展
求几何图形面积的常用方法:
(1)相加法,求全面积,如图1;
(2)相减法,求阴影部分的面积,如图2;
(3)直接求面积法,求阴影部分的面积,如图3;


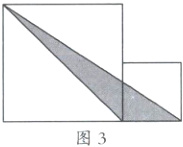
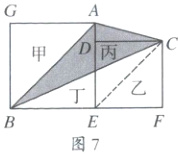
(4)重新组合法,这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可,如图4和图5,拆开图形,使阴影部分分布在正方形的4个角处;如图6和图7,根据梯形两侧三角形面积相等原理(梯形蝴蝶定理),可用三角形丁的面积替换丙的面积,组成一个大$\triangle ABE$,这样整个阴影部分面积恰是大正方形面积的一半;



(5)割补法,这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决,如图8;

(6)平移法,这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积,如图9;
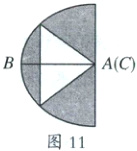
(7)旋转法,这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一直线旋转一定角度贴补在图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积,如图10和图11;

(8)对称添加法,这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半,如图12和图13;


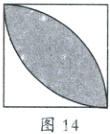
(9)重叠法,这种方法是将所求的图形看成是两个或两个以上图形的重叠部分,如图14,可先求两个扇形面积的和,再减去正方形面积,阴影部分的面积恰好是两个扇形重叠的部分.
10 D 【解析】矩形的性质+正方形的判定与性质+三角形的面积公式+相似三角形的判定与性质
[第1步,证明四边形$ABEF$是正方形]
$\because$四边形$ABCD$是矩形,$\therefore \angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ}$. $\because EF \perp BC$,$\therefore \angle BEF = \angle CEF = 90^{\circ}$. $\therefore$四边形$ABEF$和四边形$CDFE$都是矩形(关键:根据已知条件判定特殊四边形). 又$\because BE = AB$,$\therefore$四边形$ABEF$是正方形.
[第2步,证明$\triangle AGF \sim \triangle CGE$,表示出$GE$的长]
设$BE = EF = AF = a$,$CE = b$,$GE = x$(方法:根据线段长度不同设未知参数,结合图形特征建立等量关系式),$\therefore GF = EF - GE = a - x$. $\because AD // BC$,$\therefore \triangle AGF \sim \triangle CGE$. $\therefore \frac{AF}{CE} = \frac{GF}{GE}$,即$\frac{a}{b} = \frac{a - x}{x}$,$\therefore x = \frac{ab}{a + b}$(重点:当等式中出现三个未知参数,且存在等量关系时,常采用消元法,即利用等式的性质消去某一个未知数).
[第3步,利用分割法求阴影部分的面积,结合矩形$CDFE$的面积可得$S_{阴影} = \frac{1}{2} S_{矩形CDFE}$]
$\therefore S_{\triangle BEG} = \frac{1}{2} BE · GE = \frac{1}{2} ax$,$S_{\triangle DEG} = \frac{1}{2} GE · EC = \frac{1}{2} bx$.
$\therefore S_{阴影} = S_{\triangle BEG} + S_{\triangle DEG} = \frac{1}{2} x(a + b) = \frac{1}{2} ab$. 又$\because S_{矩形CDFE} = ab$,$\therefore S_{阴影} = \frac{1}{2} S_{矩形CDFE}$. $\therefore$若求阴影部分的面积,则只需要知道四边形$CDFE$的面积. 故选D.
知识拓展
求几何图形面积的常用方法:
(1)相加法,求全面积,如图1;
(2)相减法,求阴影部分的面积,如图2;
(3)直接求面积法,求阴影部分的面积,如图3;



(4)重新组合法,这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可,如图4和图5,拆开图形,使阴影部分分布在正方形的4个角处;如图6和图7,根据梯形两侧三角形面积相等原理(梯形蝴蝶定理),可用三角形丁的面积替换丙的面积,组成一个大$\triangle ABE$,这样整个阴影部分面积恰是大正方形面积的一半;




(5)割补法,这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决,如图8;

(6)平移法,这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积,如图9;
(7)旋转法,这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一直线旋转一定角度贴补在图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积,如图10和图11;


(8)对称添加法,这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半,如图12和图13;



(9)重叠法,这种方法是将所求的图形看成是两个或两个以上图形的重叠部分,如图14,可先求两个扇形面积的和,再减去正方形面积,阴影部分的面积恰好是两个扇形重叠的部分.
11. 端午节吃粽子是我国传统习俗,小瓯为全家人蒸了 2 个红枣粽,3 个肉粽,妈妈随机选了一个,则妈妈吃到红枣粽的概率是
$\frac{2}{5}$
.
答案:
11 $\frac{2}{5}$ 【考点】概率公式
12. 不等式组$\begin{cases}3x + 2 > x,\\\dfrac{1}{3}x\leqslant2\end{cases}$的解集为______.
答案:
12 $-1 < x \leq 6$ 【解析】解一元一次不等式组 解不等式$3x + 2 > x$得$x > -1$,解不等式$\frac{1}{3}x \leq 2$得$x \leq 6$,$\therefore$不等式组的解集是$-1 < x \leq 6$.
13. 如图,已知$\angle 1 = \angle 2$,若要使得$\triangle ABD\cong\triangle ACD$,则可添加的条件是
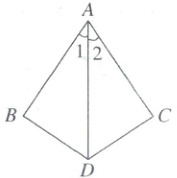
$AB = AC$(或$\angle B = \angle C$或$\angle ADB = \angle ADC$)
. (只需填写一个条件)
答案:
13 $AB = AC$(或$\angle B = \angle C$或$\angle ADB = \angle ADC$)【解析】全等三角形的判定 本题答案不唯一,可补充条件$AB = AC$,在$\triangle ABD$和$\triangle ACD$中,$\begin{cases} AB = AC, \\ \angle 1 = \angle 2, \\ AD = AD, \end{cases} \therefore \triangle ABD \cong \triangle ACD$(SAS). 可补充条件$\angle B = \angle C$,在$\triangle ABD$和$\triangle ACD$中,$\begin{cases} \angle B = \angle C, \\ \angle 1 = \angle 2, \\ AD = AD, \end{cases} \therefore \triangle ABD \cong \triangle ACD$(AAS). 可补充条件$\angle ADB = \angle ADC$,在$\triangle ABD$和$\triangle ACD$中,$\begin{cases} \angle 1 = \angle 2, \\ AD = AD, \\ \angle ADB = \angle ADC, \end{cases} \therefore \triangle ABD \cong \triangle ACD$(ASA).
14. 若扇形的圆心角为$45^{\circ}$,半径为 3,则该扇形的弧长为
$\frac{3}{4}\pi$
.
答案:
14 $\frac{3}{4}\pi$ 【解析】弧长公式 由题知,$l = \frac{45 × \pi × 3}{180} = \frac{3}{4}\pi$.
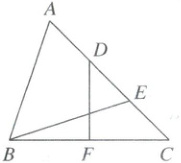
15. 如图,在$\triangle ABC$中,$\angle C = 45^{\circ}$,$AC = 6$,点$D$,$E$把线段$AC$三等分,$F$是$BC$边上的中点,连接$BE$,$DF$. 若$BE = AB$,则$DF$的长为________.

答案:
15 $2\sqrt{2}$ 【解析】等腰三角形的性质+等腰直角三角形的判定与性质 如图,连接$BD$(巧作辅助线:连接线段,构造等腰直角三角形,为解直角三角形提供条件),$\because$点$D$,$E$把线段$AC$三等分,$\therefore EC = DE = AD = \frac{1}{3} AC = \frac{1}{3} × 6 = 2$. $\therefore DC = 2EC = 4$. $\because BE = AB$,$AD = DE$,$\therefore BD \perp AE$(技巧:当遇到等腰三角形且需要研究底边相关线段或角度时,常见思路是利用“三线合一”的性质). $\therefore \angle BDC = 90^{\circ}$. 又$\because \angle C = 45^{\circ}$,$\therefore \triangle DBC$是等腰直角三角形. $\because F$是$BC$的中点,$\therefore DF \perp BC$. $\therefore \angle DFC = 90^{\circ}$. $\therefore DF = DC · \sin C = 4 × \frac{\sqrt{2}}{2} = 2\sqrt{2}$.

15 $2\sqrt{2}$ 【解析】等腰三角形的性质+等腰直角三角形的判定与性质 如图,连接$BD$(巧作辅助线:连接线段,构造等腰直角三角形,为解直角三角形提供条件),$\because$点$D$,$E$把线段$AC$三等分,$\therefore EC = DE = AD = \frac{1}{3} AC = \frac{1}{3} × 6 = 2$. $\therefore DC = 2EC = 4$. $\because BE = AB$,$AD = DE$,$\therefore BD \perp AE$(技巧:当遇到等腰三角形且需要研究底边相关线段或角度时,常见思路是利用“三线合一”的性质). $\therefore \angle BDC = 90^{\circ}$. 又$\because \angle C = 45^{\circ}$,$\therefore \triangle DBC$是等腰直角三角形. $\because F$是$BC$的中点,$\therefore DF \perp BC$. $\therefore \angle DFC = 90^{\circ}$. $\therefore DF = DC · \sin C = 4 × \frac{\sqrt{2}}{2} = 2\sqrt{2}$.

16. 如图,在菱形$ABCD$中,点$E$在对角线$BD$上,$BE = 8$,$DE = 2$,将边$AB$平移至$EF$,点$A$的对应点为点$E$,连接$BF$,若$\angle F = 90^{\circ}$,则$AB$的长为________.
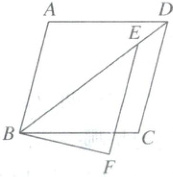

答案:
16 $2\sqrt{10}$ 【解析】菱形的性质+图形的平移变换及其性质+矩形的判定与性质+相似三角形的判定与性质+勾股定理
[第1步,延长$BF$交$DC$于点$H$,连接$AE$并延长交$CD$于点$G$,证明四边形$ABFE$是矩形,$\triangle GDE \sim \triangle ABE$,由相似三角形的性质求$\frac{GD}{AB}$]
如图,延长$BF$交$DC$的延长线于点$H$,连接$AE$并延长交$CD$于点$G$(巧作辅助线:作延长线,构造直角三角形和矩形,为证明相似三角形提供条件)(难点:当题目中出现平移线段问题,常需要补全平移图形,利用平移的性质得数量关系与位置关系). 由平移的性质得$AB // EF$,$AB = EF$,$\therefore$四边形$ABFE$是平行四边形. $\because \angle BFE = 90^{\circ}$,$\therefore$平行四边形$ABFE$是矩形. $\therefore \angle AEF = \angle FEG = 90^{\circ}$,$AG // BH$. $\because$四边形$ABCD$是菱形,$\therefore AB = BC = CD = AD$,$AB // CD$. $\therefore EF // CD$. $\therefore \angle AGD = \angle FEG = 90^{\circ}$,$\angle H = \angle BFE = 90^{\circ}$. $\because AB // CD$,$\therefore \triangle GDE \sim \triangle ABE$. $\therefore \frac{GD}{AB} = \frac{DE}{BE} = \frac{2}{8} = \frac{1}{4}$.
[第2步,设$GD = a$,根据勾股定理、平行四边形的判定与性质求$GH$,$BH$,$DH$]
设$GD = a$(技巧:对于存在线段比例关系的题目,设出其中一条线段长度,然后根据图形性质和已知条件表示出其他线段长度,能使数量关系更加清晰,方便后续计算和推理),则$AB = 4a$,$\therefore AD = AB = 4a$. 在$Rt \triangle AGD$中,由勾股定理得$AG = \sqrt{AD^2 - GD^2} = \sqrt{(4a)^2 - a^2} = \sqrt{15}a$. $\because AG // BH$,$AB // CD$,$\therefore$四边形$ABHG$是平行四边形. $\therefore GH = AB = 4a$,$BH = AG = \sqrt{15}a$. $\therefore DH = GH + GD = 4a + a = 5a$.
[第3步,根据勾股定理求$BD$,结合已知建立方程求$a$的值,可得$AB$的长]
在$Rt \triangle BDH$中,由勾股定理得$BD = \sqrt{BH^2 + DH^2} = \sqrt{(\sqrt{15}a)^2 + (5a)^2} = 2\sqrt{10}a$. $\because BD = BE + DE = 10$,$\therefore 10 = 2\sqrt{10}a$,解得$a = \frac{\sqrt{10}}{2}$. $\therefore AB = 4a = 2\sqrt{10}$.

16 $2\sqrt{10}$ 【解析】菱形的性质+图形的平移变换及其性质+矩形的判定与性质+相似三角形的判定与性质+勾股定理
[第1步,延长$BF$交$DC$于点$H$,连接$AE$并延长交$CD$于点$G$,证明四边形$ABFE$是矩形,$\triangle GDE \sim \triangle ABE$,由相似三角形的性质求$\frac{GD}{AB}$]
如图,延长$BF$交$DC$的延长线于点$H$,连接$AE$并延长交$CD$于点$G$(巧作辅助线:作延长线,构造直角三角形和矩形,为证明相似三角形提供条件)(难点:当题目中出现平移线段问题,常需要补全平移图形,利用平移的性质得数量关系与位置关系). 由平移的性质得$AB // EF$,$AB = EF$,$\therefore$四边形$ABFE$是平行四边形. $\because \angle BFE = 90^{\circ}$,$\therefore$平行四边形$ABFE$是矩形. $\therefore \angle AEF = \angle FEG = 90^{\circ}$,$AG // BH$. $\because$四边形$ABCD$是菱形,$\therefore AB = BC = CD = AD$,$AB // CD$. $\therefore EF // CD$. $\therefore \angle AGD = \angle FEG = 90^{\circ}$,$\angle H = \angle BFE = 90^{\circ}$. $\because AB // CD$,$\therefore \triangle GDE \sim \triangle ABE$. $\therefore \frac{GD}{AB} = \frac{DE}{BE} = \frac{2}{8} = \frac{1}{4}$.
[第2步,设$GD = a$,根据勾股定理、平行四边形的判定与性质求$GH$,$BH$,$DH$]
设$GD = a$(技巧:对于存在线段比例关系的题目,设出其中一条线段长度,然后根据图形性质和已知条件表示出其他线段长度,能使数量关系更加清晰,方便后续计算和推理),则$AB = 4a$,$\therefore AD = AB = 4a$. 在$Rt \triangle AGD$中,由勾股定理得$AG = \sqrt{AD^2 - GD^2} = \sqrt{(4a)^2 - a^2} = \sqrt{15}a$. $\because AG // BH$,$AB // CD$,$\therefore$四边形$ABHG$是平行四边形. $\therefore GH = AB = 4a$,$BH = AG = \sqrt{15}a$. $\therefore DH = GH + GD = 4a + a = 5a$.
[第3步,根据勾股定理求$BD$,结合已知建立方程求$a$的值,可得$AB$的长]
在$Rt \triangle BDH$中,由勾股定理得$BD = \sqrt{BH^2 + DH^2} = \sqrt{(\sqrt{15}a)^2 + (5a)^2} = 2\sqrt{10}a$. $\because BD = BE + DE = 10$,$\therefore 10 = 2\sqrt{10}a$,解得$a = \frac{\sqrt{10}}{2}$. $\therefore AB = 4a = 2\sqrt{10}$.

17. (本小题满分 8 分)计算:$(\sqrt{2})^{2}-(\dfrac{1}{3})^{0}+\sqrt[3]{8}$.
答案:
17 实数的运算
解:原式$= 2 - 1 + 2$
$= 3$.
解:原式$= 2 - 1 + 2$
$= 3$.
查看更多完整答案,请扫码查看


