《2026年天利38套中考试题精选数学浙江专版》

21. (本小题满分8分)春节期间,人工智能题材新闻密集发酵,Deepseek广受关注,相关话题讨论持续火热.某校为了培养学生对人工智能的学习兴趣,丰富学生的视野,计划组织学生进行“人工智能知识竞赛”.王老师为了从甲、乙两名同学中选择一名同学代表班级参赛,让他们进行了十次模拟答题,并绘制了如下的成绩统计图和统计表.

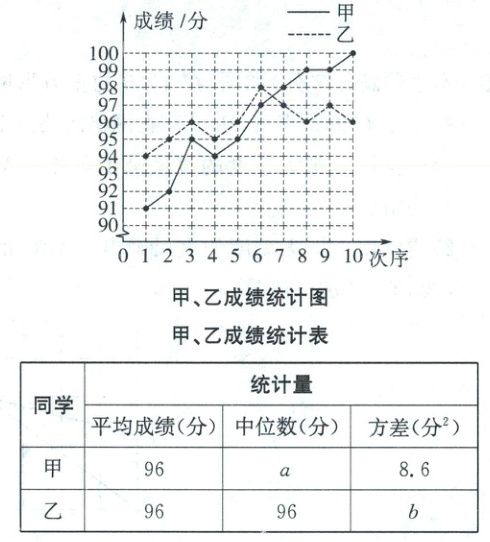
(1)求$a$与$b$的值.
(2)若乙第11次模拟答题的成绩为96分,则乙成绩的方差将____________（填“变大”“变小”或“不变”）.
(3)假如你是王老师,你会选择哪位同学代表班级参赛?请说明理由.
21.方差+平均数+中位数
解：
(1)甲的成绩为$91$，$92$，$95$，$94$，$95$，$97$，$98$，$99$，$99$，$100$，
∴甲的成绩从小到大排列为$91$，$92$，$94$，$95$，$95$，$97$，$98$，$99$，$99$，$100$.
∴$a = \frac{95 + 97}{2} = 96$.（2分）
乙的成绩为$94$，$95$，$96$，$95$，$96$，$98$，$97$，$96$，$97$，$96$，
$b = \frac{1}{10}×[(94 - 96)^{2} + (95 - 96)^{2}×2 + (96 - 96)^{2}×4 + (98 - 96)^{2} + (97 - 96)^{2}×2] = 1.2$（提示：方差公式：$s^{2} = \frac{1}{n}[(x_{1} - \bar{x})^{2} + (x_{2} - \bar{x})^{2} + ·s + (x_{n} - \bar{x})^{2}]$）.（4分）
(2)变小.（6分）
[解题过程]若乙第11次模拟答题的成绩为$96$分，则乙成绩的方差是原来的$\frac{10}{11}$，所以乙成绩的方差将变小.
(3)选择乙同学，理由如下：
因为甲、乙同学的平均数、中位数相同，而乙的方差比较小，成绩更稳定，所以选择乙同学参赛.（答案不唯一）（8分）

答案： 21.方差+平均数+中位数
解：
(1)甲的成绩为$91$，$92$，$95$，$94$，$95$，$97$，$98$，$99$，$99$，$100$，
∴甲的成绩从小到大排列为$91$，$92$，$94$，$95$，$95$，$97$，$98$，$99$，$99$，$100$.
∴$a = \frac{95 + 97}{2} = 96$.（2分）
乙的成绩为$94$，$95$，$96$，$95$，$96$，$98$，$97$，$96$，$97$，$96$，
$b = \frac{1}{10}×[(94 - 96)^{2} + (95 - 96)^{2}×2 + (96 - 96)^{2}×4 + (98 - 96)^{2} + (97 - 96)^{2}×2] = 1.2$（提示：方差公式：$s^{2} = \frac{1}{n}[(x_{1} - \bar{x})^{2} + (x_{2} - \bar{x})^{2} + ·s + (x_{n} - \bar{x})^{2}]$）.（4分）
(2)变小.（6分）
[解题过程]若乙第11次模拟答题的成绩为$96$分，则乙成绩的方差是原来的$\frac{10}{11}$，所以乙成绩的方差将变小.
(3)选择乙同学，理由如下：
因为甲、乙同学的平均数、中位数相同，而乙的方差比较小，成绩更稳定，所以选择乙同学参赛.（答案不唯一）（8分）

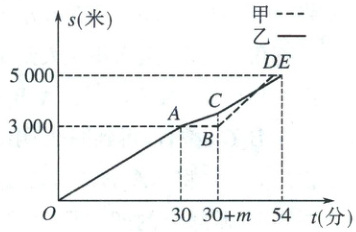
22. (本小题满分10分)某地举行机器人跑步比赛,机器人甲和乙以相同的速度同时同地同向出发,在行进30分钟时,两机器人均因机器过热发生故障.机器人甲立即停止行进,服务团队对其进行模块更换优化算法,$m$分钟后修复完成,行进速度提升了$28\%$;针对机器人乙,服务团队则让其在降低速度$50\%$的情况下继续行进自然降温,在机器人甲修复完成时,机器人乙立即恢复正常速度.比赛过程中机器人行进路程$s$(米)与时间$t$(分钟)的函数关系如图所示.
(1)求机器人乙出发时的速度.
(2)求直线$CE$的函数表达式.
(3)当机器人甲到达终点时,求机器人乙到终点的路程.

答案： 22.一次函数的实际应用
解：
(1)$3000÷30 = 100$（米/分）.
答：机器人乙出发时的速度是$100$米/分.（3分）
(2)根据题意，得$3000 + 100×(1 - 50\%)m + 100(54 - 30 - m) = 5000$（难点：要求出直线$CE$的解析式，必须求得$C$点坐标，首先求出坐标系中$m$的值，从“乙行驶的总路程=各段路程之和”列出关于$m$的方程便可突破这个难关），
解得$m = 8$，
$30 + 8 = 38$（分），
$3000 + 100×(1 - 50\%)×8 = 3400$（米），
∴$C(38, 3400)$.
$s = 3400 + 100(t - 38) = 100t - 400$.
∴直线$CE$的函数表达式为$s = 100t - 400(38 \leq t \leq 54)$.（6分）
(3)甲机器人在$BD$段所用时间为$(5000 - 3000)÷[100×(1 + 28\%)] = 15.625$（分），
$38 + 15.625 = 53.625$（分），
∴$D(53.625, 5000)$.
当$t = 53.625$时，乙机器人行进的路程为$s = 100×53.625 - 400 = 4962.5$（米），
$5000 - 4962.5 = 37.5$（米）.
答：机器人乙到终点的路程为$37.5$米.（10分）