第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
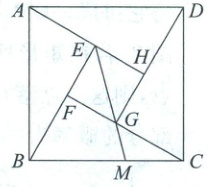
6. 如图是中国古代数学家赵爽用来证明勾股定理的弦图,它是由四个全等的直角三角形和一个小正方形$EFGH$组成,恰好拼成一个大正方形$ABCD$. 连接$EG$并延长交$BC$于点$M$. 若$AB = \sqrt{34}$,$EF = 2$,则$GM$的长为( )
A.$\frac{9}{8}\sqrt{2}$
B.$\sqrt{2}$
C.$\frac{7}{8}\sqrt{2}$
D.$\frac{4}{5}\sqrt{2}$

A.$\frac{9}{8}\sqrt{2}$
B.$\sqrt{2}$
C.$\frac{7}{8}\sqrt{2}$
D.$\frac{4}{5}\sqrt{2}$
答案:
6.A [解析] 正方形的性质+等腰直角三角形的判定与性质+勾股定理+锐角三角函数
∵大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成,
∴AE = BF = GC = DH。设AE = x,在Rt△AEB中,AB = $\sqrt{34}$,BE = EF + BF = 2 + x。由勾股定理得AB² = AE² + BE²,即($\sqrt{34}$)² = x² + (2 + x)²,解得x₁ = 3,x₂ = −5(舍去),则BF = GC = 3。如图,过点M作MN⊥FC于点N(巧作辅助线:作垂线,构造直角三角形)(技巧:当已知图形中出现30°,45°,60°的角时,若求边长,一般会应用特殊角的三角函数值,则需要将特殊角放置在直角三角形内,如本题中的辅助线)。由题知,△EFG为等腰直角三角形(提示:正方形的对角线将正方形分成两个全等的等腰直角三角形),
∴∠NGM = ∠EGF = 45°,
∴△GNM为等腰直角三角形。设GN = NM = a,则NC = GC−GN = 3−a,
∴tan∠FCB = $\frac{BF}{CF}$ = $\frac{NM}{NC}$,即$\frac{3}{3 + 2}$ = $\frac{a}{3−a}$,解得a = $\frac{9}{8}$。
∴GM = $\sqrt{2}$GN = $\frac{9}{8}$$\sqrt{2}$。故选A。

6.A [解析] 正方形的性质+等腰直角三角形的判定与性质+勾股定理+锐角三角函数
∵大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成,
∴AE = BF = GC = DH。设AE = x,在Rt△AEB中,AB = $\sqrt{34}$,BE = EF + BF = 2 + x。由勾股定理得AB² = AE² + BE²,即($\sqrt{34}$)² = x² + (2 + x)²,解得x₁ = 3,x₂ = −5(舍去),则BF = GC = 3。如图,过点M作MN⊥FC于点N(巧作辅助线:作垂线,构造直角三角形)(技巧:当已知图形中出现30°,45°,60°的角时,若求边长,一般会应用特殊角的三角函数值,则需要将特殊角放置在直角三角形内,如本题中的辅助线)。由题知,△EFG为等腰直角三角形(提示:正方形的对角线将正方形分成两个全等的等腰直角三角形),
∴∠NGM = ∠EGF = 45°,
∴△GNM为等腰直角三角形。设GN = NM = a,则NC = GC−GN = 3−a,
∴tan∠FCB = $\frac{BF}{CF}$ = $\frac{NM}{NC}$,即$\frac{3}{3 + 2}$ = $\frac{a}{3−a}$,解得a = $\frac{9}{8}$。
∴GM = $\sqrt{2}$GN = $\frac{9}{8}$$\sqrt{2}$。故选A。

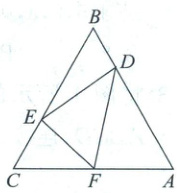
1. 如图,在$\triangle ABC$中,$AB = BC = AC$,点$F$为$AC$边上的中点,以$F$为顶点作一个$60^{\circ}$的角交$AB$,$BC$边于$D$,$E$两点,连接$DE$,则知道下列哪个条件就可以计算$\triangle ABC$的周长( )
A.$\triangle ADF$的周长
B.$\triangle BDE$的周长
C.$\triangle CEF$的周长
D.$\triangle DEF$的周长

A.$\triangle ADF$的周长
B.$\triangle BDE$的周长
C.$\triangle CEF$的周长
D.$\triangle DEF$的周长
答案:
1.B [解析] 等边三角形的性质+全等三角形的判定与性质+相似三角形的判定与性质
【思维导图】取AB中点G,连接FG,在ED上截取EH = EC,连接FH→△CEF∽△AFD→△CEF∽△FED→△ECF≌△EHF→DG = DH→C△BDE = $\frac{3}{2}$BC→得解。
如图,取AB中点G,连接FG,在ED上截取EH = EC,连接FH。
∵AB = BC = AC,
∴∠A = ∠C = 60°。
∵∠EFD = 60°,
∴∠EFC + ∠FEC = ∠EFC + ∠AFD = 120°。
∴∠FEC = ∠AFD。
∴△CEF∽△AFD。
∴$\frac{EF}{FD}$ = $\frac{CE}{AF}$。
∵F为AC边上的中点,
∴AF = CF。
∴$\frac{EF}{FD}$ = $\frac{CE}{CF}$。
∵∠EFD = ∠ECF,
∴△CEF∽△FED。
∴△CEF∽△FED∽△AFD,∠CEF = ∠FED。在△ECF和△EHF中,$\begin{cases} EC = EH\\ ∠CEF = ∠HEF\\ EF = EF \end{cases}$,
∴△ECF≌△EHF(SAS)。
∴∠FHE = ∠ECF = 60°。又易知FG是△ABC的中位线,
∴∠FGA = ∠B = 60°。
∴∠FHD = ∠FGD = 120°。由△FED∽△AFD可知∠FDH = ∠FDG。又FD = FD,
∴△FDH≌△FDG(AAS)。
∴DG = DH。
∴C△BDE = BE + DE + BD = BE + EH + DH + BD = BC + BG = $\frac{3}{2}$BC,即为△ABC周长的一半。故选B。

1.B [解析] 等边三角形的性质+全等三角形的判定与性质+相似三角形的判定与性质
【思维导图】取AB中点G,连接FG,在ED上截取EH = EC,连接FH→△CEF∽△AFD→△CEF∽△FED→△ECF≌△EHF→DG = DH→C△BDE = $\frac{3}{2}$BC→得解。
如图,取AB中点G,连接FG,在ED上截取EH = EC,连接FH。
∵AB = BC = AC,
∴∠A = ∠C = 60°。
∵∠EFD = 60°,
∴∠EFC + ∠FEC = ∠EFC + ∠AFD = 120°。
∴∠FEC = ∠AFD。
∴△CEF∽△AFD。
∴$\frac{EF}{FD}$ = $\frac{CE}{AF}$。
∵F为AC边上的中点,
∴AF = CF。
∴$\frac{EF}{FD}$ = $\frac{CE}{CF}$。
∵∠EFD = ∠ECF,
∴△CEF∽△FED。
∴△CEF∽△FED∽△AFD,∠CEF = ∠FED。在△ECF和△EHF中,$\begin{cases} EC = EH\\ ∠CEF = ∠HEF\\ EF = EF \end{cases}$,
∴△ECF≌△EHF(SAS)。
∴∠FHE = ∠ECF = 60°。又易知FG是△ABC的中位线,
∴∠FGA = ∠B = 60°。
∴∠FHD = ∠FGD = 120°。由△FED∽△AFD可知∠FDH = ∠FDG。又FD = FD,
∴△FDH≌△FDG(AAS)。
∴DG = DH。
∴C△BDE = BE + DE + BD = BE + EH + DH + BD = BC + BG = $\frac{3}{2}$BC,即为△ABC周长的一半。故选B。

2. 在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB > AC$,分别以$AB$,$AC$为边向外作正方形$ABDE$,$ACFG$. 连接$EG$,过点$B$作$BH \perp EG$于点$H$,过点$A$作$MN // BC$分别交$BD$,$FG$,$BH$于点$M$,$N$,$P$. 则下列比值为定值的是( )
A.$\frac{AP}{EG}$
B.$\frac{BH}{EG}$
C.$\frac{MN}{EG}$
D.$\frac{PH}{EG}$
A.$\frac{AP}{EG}$
B.$\frac{BH}{EG}$
C.$\frac{MN}{EG}$
D.$\frac{PH}{EG}$
答案:
2.A [解析] 正方形的性质+全等三角形的判定与性质+平行四边形的判定与性质+等角对等边
第1步,证明△ABC≌△AEG
设BH交AE于点K,如图所示,
∵四边形ABDE、四边形ACFG都是正方形,
∴AB = AE,AC = AG,∠ABD = ∠BAE = 90°。又
∵∠BAC = ∠EAG = 90°,
∴△ABC≌△AEG(SAS)。
第2步,证明四边形ACBM是平行四边形,得对应边相等
∴∠ABC = ∠AEG,BC = EG。
∵∠BAC = ∠ABD = 90°,
∴AC//BM。又
∵MN//BC,
∴四边形ACBM是平行四边形。
∴AM = BC。
∴AM = EG。
第3步,根据等角对等边得边长相等,从而可得$\frac{AP}{EG}$为定值
∵BH⊥EG,
∴∠EHK = ∠BAE = 90°。
∴∠AEG + ∠1 = ∠ABP + ∠2 = 90°。又
∵∠1 = ∠2,
∴∠AEG = ∠ABP。
∵MN//BC,
∴∠PAB = ∠ABC。又
∵∠ABC = ∠AEG,
∴∠PAB = ∠ABP。
∴AP = PB。
∵∠3 + ∠PAB = 90°,∠4 + ∠ABP = 90°,
∴∠3 = ∠4。
∴PB = PM。
∴AP = PM。
∴AM = 2AP。
∴EG = 2AP。
∴$\frac{AP}{EG}$ = $\frac{1}{2}$,为定值。故选A。

2.A [解析] 正方形的性质+全等三角形的判定与性质+平行四边形的判定与性质+等角对等边
第1步,证明△ABC≌△AEG
设BH交AE于点K,如图所示,
∵四边形ABDE、四边形ACFG都是正方形,
∴AB = AE,AC = AG,∠ABD = ∠BAE = 90°。又
∵∠BAC = ∠EAG = 90°,
∴△ABC≌△AEG(SAS)。
第2步,证明四边形ACBM是平行四边形,得对应边相等
∴∠ABC = ∠AEG,BC = EG。
∵∠BAC = ∠ABD = 90°,
∴AC//BM。又
∵MN//BC,
∴四边形ACBM是平行四边形。
∴AM = BC。
∴AM = EG。
第3步,根据等角对等边得边长相等,从而可得$\frac{AP}{EG}$为定值
∵BH⊥EG,
∴∠EHK = ∠BAE = 90°。
∴∠AEG + ∠1 = ∠ABP + ∠2 = 90°。又
∵∠1 = ∠2,
∴∠AEG = ∠ABP。
∵MN//BC,
∴∠PAB = ∠ABC。又
∵∠ABC = ∠AEG,
∴∠PAB = ∠ABP。
∴AP = PB。
∵∠3 + ∠PAB = 90°,∠4 + ∠ABP = 90°,
∴∠3 = ∠4。
∴PB = PM。
∴AP = PM。
∴AM = 2AP。
∴EG = 2AP。
∴$\frac{AP}{EG}$ = $\frac{1}{2}$,为定值。故选A。

3. 如图,在$\triangle ABC$中,点$D$是$AB$上一点(不与点$A$,$B$重合),过点$D$作$DE // BC$交$AC$于点$E$,过点$E$作$EF // AB$交$BC$于点$F$,点$G$是线段$DE$上一点,$EG = 2DG$,点$H$是线段$CF$上一点,$CH = 2HF$. 连接$AG$,$AH$,$GH$,$HF$. 若已知$\triangle AGH$的面积,则一定能求出(
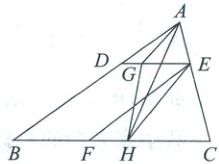
A.$\triangle ABC$的面积
B.$\triangle ADE$的面积
C.四边形$DBFE$的面积
D.$\triangle EFC$的面积
B
)
A.$\triangle ABC$的面积
B.$\triangle ADE$的面积
C.四边形$DBFE$的面积
D.$\triangle EFC$的面积
答案:
3.B [解析] 相似三角形的判定与性质+平行线的判定与性质+三角形的面积
【思维导图】已知条件→△ADE∽△EFC→$\frac{AD}{EF}$ = $\frac{DE}{FC}$→△ADG∽△EFH→∠DAG = ∠FEH→AG//EH→S△AGH = S△AEG→$\frac{EG}{DE}$ = $\frac{2}{3}$→$\frac{S△AEG}{S△ADE}$ = $\frac{EG}{DE}$→得解。
∵DE//BC,
∴∠AED = ∠C,∠ADE = ∠B。
∵EF//AB,
∴∠B = ∠EFC,
∴∠ADE = ∠EFC,
∴△ADE∽△EFC,
∴$\frac{AD}{EF}$ = $\frac{DE}{FC}$。
∵EG = 2DG,CH = 2HF,
∴DG = $\frac{1}{3}$DE,FH = $\frac{1}{3}$FC。
∴$\frac{DG}{FH}$ = $\frac{DE}{FC}$。
∴$\frac{AD}{EF}$ = $\frac{DG}{FH}$。
∵∠ADG = ∠EFH,
∴△ADG∽△EFH,
∴∠DAG = ∠FEH。
∵EF//AB,
∴∠DAE = ∠FEC,
∴∠DAE−∠DAG = ∠FEC−∠FEH,即∠GAE = ∠HEC,
∴AG//EH。
∴S△AGH = S△AEG。
∵EG = 2DG,
∴$\frac{EG}{DE}$ = $\frac{2}{3}$。
∴$\frac{S△AEG}{S△ADE}$ = $\frac{EG}{DE}$。
∴$S_{△ADE}$ = $\frac{3}{2}$$S_{△AEG}$。
∴$S_{△ADE}$ = $\frac{3}{2}$$S_{△AGH}$。已知△AGH的面积,则一定能求出△ADE的面积。故选B。
【思维导图】已知条件→△ADE∽△EFC→$\frac{AD}{EF}$ = $\frac{DE}{FC}$→△ADG∽△EFH→∠DAG = ∠FEH→AG//EH→S△AGH = S△AEG→$\frac{EG}{DE}$ = $\frac{2}{3}$→$\frac{S△AEG}{S△ADE}$ = $\frac{EG}{DE}$→得解。
∵DE//BC,
∴∠AED = ∠C,∠ADE = ∠B。
∵EF//AB,
∴∠B = ∠EFC,
∴∠ADE = ∠EFC,
∴△ADE∽△EFC,
∴$\frac{AD}{EF}$ = $\frac{DE}{FC}$。
∵EG = 2DG,CH = 2HF,
∴DG = $\frac{1}{3}$DE,FH = $\frac{1}{3}$FC。
∴$\frac{DG}{FH}$ = $\frac{DE}{FC}$。
∴$\frac{AD}{EF}$ = $\frac{DG}{FH}$。
∵∠ADG = ∠EFH,
∴△ADG∽△EFH,
∴∠DAG = ∠FEH。
∵EF//AB,
∴∠DAE = ∠FEC,
∴∠DAE−∠DAG = ∠FEC−∠FEH,即∠GAE = ∠HEC,
∴AG//EH。
∴S△AGH = S△AEG。
∵EG = 2DG,
∴$\frac{EG}{DE}$ = $\frac{2}{3}$。
∴$\frac{S△AEG}{S△ADE}$ = $\frac{EG}{DE}$。
∴$S_{△ADE}$ = $\frac{3}{2}$$S_{△AEG}$。
∴$S_{△ADE}$ = $\frac{3}{2}$$S_{△AGH}$。已知△AGH的面积,则一定能求出△ADE的面积。故选B。
4. 如图,点$E$,$F$,$M$,$N$分别在菱形$ABCD$的边$AB$,$BC$,$AD$,$CD$上,连接$EF$,$MN$,若$AB = 5$,$BE = BF = AM = CN$,$\sin B = x\sin\angle EFB$,记$EF + MN = y$,当$x$,$y$发生变化时,下列代数式的值不变的是( )

A.$\frac{y}{x}$
B.$\frac{y}{x^2}$
C.$xy$
D.$y - x$

A.$\frac{y}{x}$
B.$\frac{y}{x^2}$
C.$xy$
D.$y - x$
答案:
4.A [解析] 菱形的性质+锐角三角函数+相似三角形的判定与性质 过点E作EP⊥BF于点P,连接AC,如图所示,则△BEP和△EFP都是直角三角形。设BE = BF = AM = CN = a,在Rt△BEP中,sinB = $\frac{EP}{BE}$ = $\frac{EP}{a}$,在Rt△EFP中,sin∠EFB = $\frac{EP}{EF}$。
∵sinB = xsin∠EFB,
∴$\frac{EP}{a}$ = x⋅$\frac{EP}{EF}$,
∴EF = ax。
∵四边形ABCD是菱形,且AB = 5,
∴CB = AD = CD = AB = 5。
∵∠B = ∠D,∠BAC = ∠DAC。
∴AE = CF = DM = DN = 5−a。
∵BE = BF = a,AB = CB = 5,
∴$\frac{BE}{AB}$ = $\frac{BF}{CB}$ = $\frac{a}{5}$。又∠EBF = ∠ABC,
∴△BEF∽△BAC。
∴∠BEF = ∠BAC。同理,△DMN∽△DAC,
∴∠DMN = ∠DAC。
∵∠BAC = ∠DAC,
∴∠BEF = ∠DMN。又∠B = ∠D,
∴△BEF∽△DMN。
∴$\frac{EF}{MN}$ = $\frac{BE}{DM}$。
∴$\frac{ax}{MN}$ = $\frac{a}{5−a}$。
∴MN = 5x−ax。
∴y = EF + MN = ax + 5x−ax = 5x。
∴$\frac{y}{x}$ = 5。当x,y发生变化时,$\frac{y}{x}$的值不变。故选A。

4.A [解析] 菱形的性质+锐角三角函数+相似三角形的判定与性质 过点E作EP⊥BF于点P,连接AC,如图所示,则△BEP和△EFP都是直角三角形。设BE = BF = AM = CN = a,在Rt△BEP中,sinB = $\frac{EP}{BE}$ = $\frac{EP}{a}$,在Rt△EFP中,sin∠EFB = $\frac{EP}{EF}$。
∵sinB = xsin∠EFB,
∴$\frac{EP}{a}$ = x⋅$\frac{EP}{EF}$,
∴EF = ax。
∵四边形ABCD是菱形,且AB = 5,
∴CB = AD = CD = AB = 5。
∵∠B = ∠D,∠BAC = ∠DAC。
∴AE = CF = DM = DN = 5−a。
∵BE = BF = a,AB = CB = 5,
∴$\frac{BE}{AB}$ = $\frac{BF}{CB}$ = $\frac{a}{5}$。又∠EBF = ∠ABC,
∴△BEF∽△BAC。
∴∠BEF = ∠BAC。同理,△DMN∽△DAC,
∴∠DMN = ∠DAC。
∵∠BAC = ∠DAC,
∴∠BEF = ∠DMN。又∠B = ∠D,
∴△BEF∽△DMN。
∴$\frac{EF}{MN}$ = $\frac{BE}{DM}$。
∴$\frac{ax}{MN}$ = $\frac{a}{5−a}$。
∴MN = 5x−ax。
∴y = EF + MN = ax + 5x−ax = 5x。
∴$\frac{y}{x}$ = 5。当x,y发生变化时,$\frac{y}{x}$的值不变。故选A。

1. (2025·广东)如图,在矩形$ABCD$中,$E$,$F$是$BC$边上的三等分点,连接$DE$,$AF$相交于点$G$,连接$CG$. 若$AB = 8$,$BC = 12$,

A.$\frac{\sqrt{10}}{10}$
B.$\frac{1}{3}$
C.$\frac{3\sqrt{10}}{10}$
D.$\frac{2}{3}$
则
$\tan\angle GCF$的值是( )
A.$\frac{\sqrt{10}}{10}$
B.$\frac{1}{3}$
C.$\frac{3\sqrt{10}}{10}$
D.$\frac{2}{3}$
答案:
1.B [解析] 矩形的性质+等腰直角三角形的判定和性质+锐角三角函数
第1步,作GH⊥BC,由已知条件判断△ABF,△CDE,△GEF是等腰直角三角形
如图,过点G作GH⊥BC于点H,在矩形ABCD中,AB = 8,BC = 12,∠B = 90°。
∵点E,F是BC的三等分点,
∴BE = EF = CF = $\frac{1}{3}$BC = 4。
∴BF = BE + EF = 8。
∴AB = BF = 8。
∴△ABF是等腰直角三角形。
∴∠BFA = 45°。同理△CDE是等腰直角三角形。
∴∠CED = 45°。
∴∠BFA = ∠CED。
∴△GEF是等腰直角三角形。
第2步,由等腰直角三角形的性质求GH,CH的长,从而求得tan∠GCF的值
∵GH⊥EF,
∴GH = EH = FH = $\frac{1}{2}$EF = 2。
∴CH = CF + HF = 4 + 2 = 6。在Rt△GHC中,tan∠GCF = $\frac{GH}{CH}$ = $\frac{2}{6}$ = $\frac{1}{3}$。故选B。

1.B [解析] 矩形的性质+等腰直角三角形的判定和性质+锐角三角函数
第1步,作GH⊥BC,由已知条件判断△ABF,△CDE,△GEF是等腰直角三角形
如图,过点G作GH⊥BC于点H,在矩形ABCD中,AB = 8,BC = 12,∠B = 90°。
∵点E,F是BC的三等分点,
∴BE = EF = CF = $\frac{1}{3}$BC = 4。
∴BF = BE + EF = 8。
∴AB = BF = 8。
∴△ABF是等腰直角三角形。
∴∠BFA = 45°。同理△CDE是等腰直角三角形。
∴∠CED = 45°。
∴∠BFA = ∠CED。
∴△GEF是等腰直角三角形。
第2步,由等腰直角三角形的性质求GH,CH的长,从而求得tan∠GCF的值
∵GH⊥EF,
∴GH = EH = FH = $\frac{1}{2}$EF = 2。
∴CH = CF + HF = 4 + 2 = 6。在Rt△GHC中,tan∠GCF = $\frac{GH}{CH}$ = $\frac{2}{6}$ = $\frac{1}{3}$。故选B。

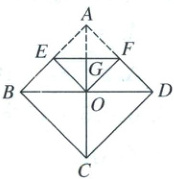
2. (2025·广东深圳)如图,将正方形$ABCD$沿$EF$折叠,使得点$A$与对角线的交点$O$重合,$EF$为折痕,则$\frac{EF}{CG}$的值为(
A.$\frac{1}{4}$
B.$\frac{1}{2}$
C.$\frac{\sqrt{2}}{2}$
D.$\frac{2}{3}$
D
)
A.$\frac{1}{4}$
B.$\frac{1}{2}$
C.$\frac{\sqrt{2}}{2}$
D.$\frac{2}{3}$
答案:
2.D [解析] 正方形的性质+折叠的性质+相似三角形的判定与性质
解法一(特殊值法):设正方形的边长为2,则BD = AC = $\sqrt{2}$AB = 2$\sqrt{2}$。根据折叠的性质可得四边形AEOF是正方形,且E,F分别是AB,AD的中点,
∴EF = $\frac{1}{2}$BD = $\sqrt{2}$,AG = OG = $\frac{1}{2}$AO = $\frac{1}{4}$AC = $\frac{\sqrt{2}}{2}$。
∴CG = AC−AG = $\frac{3\sqrt{2}}{2}$。
∴$\frac{EF}{CG}$ = $\frac{\sqrt{2}}{\frac{3\sqrt{2}}{2}}$ = $\frac{2}{3}$。故选D。
解法二(相似三角形法):
∵四边形ABCD是正方形,
∴OA = OC。根据折叠的性质可得四边形AEOF是正方形,
∴AG = OG。
∴CG = $\frac{3}{4}$AC。
∵∠BAC = ∠AEF = 45°,∠ACB = ∠AFE = ∠45°,
∴△AEF∽△BAC。
∴$\frac{EF}{AC}$ = $\frac{AE}{BA}$ = $\frac{1}{2}$。
∴EF = $\frac{1}{2}$AC。
∴$\frac{EF}{\frac{4}{3}CG}$ = $\frac{\frac{1}{2}AC}{\frac{4}{3}CG}$ = $\frac{2}{3}$。故选D。
解法一(特殊值法):设正方形的边长为2,则BD = AC = $\sqrt{2}$AB = 2$\sqrt{2}$。根据折叠的性质可得四边形AEOF是正方形,且E,F分别是AB,AD的中点,
∴EF = $\frac{1}{2}$BD = $\sqrt{2}$,AG = OG = $\frac{1}{2}$AO = $\frac{1}{4}$AC = $\frac{\sqrt{2}}{2}$。
∴CG = AC−AG = $\frac{3\sqrt{2}}{2}$。
∴$\frac{EF}{CG}$ = $\frac{\sqrt{2}}{\frac{3\sqrt{2}}{2}}$ = $\frac{2}{3}$。故选D。
解法二(相似三角形法):
∵四边形ABCD是正方形,
∴OA = OC。根据折叠的性质可得四边形AEOF是正方形,
∴AG = OG。
∴CG = $\frac{3}{4}$AC。
∵∠BAC = ∠AEF = 45°,∠ACB = ∠AFE = ∠45°,
∴△AEF∽△BAC。
∴$\frac{EF}{AC}$ = $\frac{AE}{BA}$ = $\frac{1}{2}$。
∴EF = $\frac{1}{2}$AC。
∴$\frac{EF}{\frac{4}{3}CG}$ = $\frac{\frac{1}{2}AC}{\frac{4}{3}CG}$ = $\frac{2}{3}$。故选D。
3. 如图,在菱形$ABCD$中,$O$为对角线$AC$中点,将$AB$绕顶点$A$逆时针旋转至$AE$,使$E$点恰好落在$BC$上,连接$OE$,$OD$. 若$OE \perp BC$,则$\frac{OE}{OD}$的值为( )

A.$\frac{1}{2}$
B.$\frac{\sqrt{2}}{2}$
C.$\frac{1}{3}$
D.$\frac{\sqrt{3}}{3}$

A.$\frac{1}{2}$
B.$\frac{\sqrt{2}}{2}$
C.$\frac{1}{3}$
D.$\frac{\sqrt{3}}{3}$
答案:
3.D [解析] 旋转的性质+等腰三角形的性质+相似三角形的判定和性质+菱形的性质+平行线分线段成比例定理 如图,过点A作AF⊥BC于点F,
∵OE⊥BC,
∴OE//AF。
∴$\frac{CO}{OA}$ = $\frac{CE}{EF}$。
∵O为菱形ABCD对角线AC的中点,
∴CO = OA。
∴CE = EF。
∵AB绕顶点A逆时针旋转至AE,
∴AB = AE。又
∵AF⊥BC,
∴EF = BF(提示:等腰三角形的“三线合一”性质)。
∴CE = $\frac{1}{3}$BC。
∵四边形ABCD是菱形,
∴AD = BC = 3CE,AD//CB,OD⊥AC。
∴∠DAO = ∠OCE,∠DOA = ∠OEC = 90°。
∴△DAO∽△OCE。
∴$\frac{AD}{CO}$ = $\frac{AO}{CE}$ = $\frac{OD}{OE}$。
∴$\frac{3CE}{CO}$ = $\frac{CO}{CE}$ = $\frac{OD}{OE}$。
∴OC = $\sqrt{3}$CE。
∴$\frac{\sqrt{3}CE}{CE}$ = $\frac{OD}{OE}$。
∴$\frac{OE}{OD}$ = $\frac{1}{\sqrt{3}}$ = $\frac{\sqrt{3}}{3}$。故选D。

3.D [解析] 旋转的性质+等腰三角形的性质+相似三角形的判定和性质+菱形的性质+平行线分线段成比例定理 如图,过点A作AF⊥BC于点F,
∵OE⊥BC,
∴OE//AF。
∴$\frac{CO}{OA}$ = $\frac{CE}{EF}$。
∵O为菱形ABCD对角线AC的中点,
∴CO = OA。
∴CE = EF。
∵AB绕顶点A逆时针旋转至AE,
∴AB = AE。又
∵AF⊥BC,
∴EF = BF(提示:等腰三角形的“三线合一”性质)。
∴CE = $\frac{1}{3}$BC。
∵四边形ABCD是菱形,
∴AD = BC = 3CE,AD//CB,OD⊥AC。
∴∠DAO = ∠OCE,∠DOA = ∠OEC = 90°。
∴△DAO∽△OCE。
∴$\frac{AD}{CO}$ = $\frac{AO}{CE}$ = $\frac{OD}{OE}$。
∴$\frac{3CE}{CO}$ = $\frac{CO}{CE}$ = $\frac{OD}{OE}$。
∴OC = $\sqrt{3}$CE。
∴$\frac{\sqrt{3}CE}{CE}$ = $\frac{OD}{OE}$。
∴$\frac{OE}{OD}$ = $\frac{1}{\sqrt{3}}$ = $\frac{\sqrt{3}}{3}$。故选D。

查看更多完整答案,请扫码查看


