《2026年天利38套中考试题精选数学浙江专版》

4. 如图，在$Rt\triangle ABC$中，$\angle ABC = 90^{\circ}$，$BC = 5$，$\tan A = \frac{1}{2}$，点$D$，$E$分别在$AB$，$AC$边上，将$\triangle ADE$沿$DE$翻折得到$\triangle A'DE$，$A'E$与$AB$相交于点$F$，$A'D \perp AB$. 若$\triangle BEF$与$\triangle BCE$面积相等，$AD$的长为（ ）


A.$3\sqrt{2}$
B.$\frac{10}{3}$
C.$\sqrt{5} + 1$
D.$2\sqrt{3}$

答案：
4.B [解析] 解直角三角形+折叠的性质+全等三角形的判定与性质
第1步，作EH⊥AB，证明△EDH为等腰直角三角形，得EH = DH，结合tanA = $\frac{1}{2}$，可得A'D = AD = DH = EH
如图，过点E作EH⊥AB于点H(巧作辅助线：作垂线，构造直角三角形，为通过解直角三角形求线段长做准备)(技巧：当题目已知三角函数值求线段长时，首先考虑是否需要以已知角为三角形的一个内角，通过作垂线构造直角三角形求线段长)。
∵A'D⊥AB，
∴∠A'DA = 90°。由折叠的性质可得AD = A'D，∠ADE = ∠A'DE = $\frac{360°−90°}{2}$ = 135°，
∴∠EDH = 45°。
∴△EDH为等腰直角三角形。
∴EH = DH。在Rt△AEH中，tanA = $\frac{EH}{AH}$ = $\frac{1}{2}$，
∴AH = 2EH。
∴A'D = AD = DH = EH。
第2步，根据AAS证明△DFA'≌△HFE
设A'D = AD = DH = EH = x，则DF = FH = $\frac{1}{2}$x。在Rt△ABC中，tanA = $\frac{BC}{AB}$ = $\frac{1}{2}$，
∴AB = 2BC = 10。
∴BF = AB−AD−DF = 10−$\frac{3}{2}$x，BH = AB−AD−DH = 10−2x。
∴$S_{△BEF}$ = $\frac{1}{2}$BF⋅EH = $\frac{1}{2}$(10−$\frac{3}{2}$x)⋅x，$S_{△BCE}$ = $\frac{1}{2}$BC⋅BH = $\frac{5}{2}$(10−2x) = 25−5x。
第3步，建立关于x的方程求x的值，据此可得AD的长
∵△BEF与△BCE面积相等，
∴$\frac{1}{2}$(10−$\frac{3}{2}$x)x = 25−5x，解得x = $\frac{10}{3}$或10(舍去)。
∴AD = $\frac{10}{3}$。故选B。

5. 如图，在平行四边形$ABCD$中，$BC = 4\sqrt{3}$，平行四边形$ABCD$的面积为$16\sqrt{3}$，$E$，$F$分别为边$AD$，$BC$上的点，且$AE = CF$，连接$BE$，$AF$，则$AF + BE$的最小值为（ ）


A.$8$
B.$8\sqrt{3}$
C.$16$
D.$4\sqrt{7}$

答案：
5.D [解析] 平行四边形的判定与性质+轴对称的性质+勾股定理
第1步，连接EC，作点C关于AD的对称点H，连接CH交AD于点N，连接BH，EH。由平行四边形的判定与性质求得AF = EC
如图，连接EC(巧作辅助线：构造平行四边形)，作点C关于AD对称点H，连接CH，交AD于点N，连接BH，EH(巧作辅助线：作对称，利用轴对称的性质及平行四边形的性质进行等量代换，结合三角形三边关系解题)。
∵四边形ABCD是平行四边形，
∴AD = BC = 4$\sqrt{3}$，AD//BC。又
∵AE = CF，
∴四边形AECF是平行四边形。
∴AF = EC。
第2步，根据轴对称的性质及三角形三边关系确定当B，E，H三点共线时，AF + BE取最小值
∵点C、点H关于AD对称，
∴EH = EC，CN = HN，AD⊥CH。
∴EC = AF = EH。
∴AF + BE = EH + BE。
∴当B，E，H三点共线时，AF + BE取得最小值，最小值为BH的长。
第3步，由平行四边形的面积得出CN的长，再由勾股定理得解
∵AD = 4$\sqrt{3}$，平行四边形ABCD的面积为16$\sqrt{3}$，
∴AD⋅CN = 16$\sqrt{3}$。
∴CN = 4。
∴CH = 8。
∴BH = $\sqrt{BC²+CH²}$ = $\sqrt{(4\sqrt{3})²+8²}$ = 4$\sqrt{7}$。故选D。

6. 如图，已知菱形$ABCD$的边长为$2$，$\angle DAB = 60^{\circ}$，$E$为$AB$的中点，$F$为$CE$的中点，$AF$与$DE$相交于点$G$，则$GF$的长等于（ ）


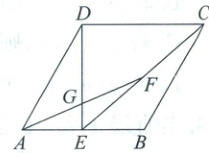
A.$1$
B.$\frac{\sqrt{3}}{2}$
C.$\frac{3\sqrt{3}}{4}$
D.$\frac{\sqrt{19}}{4}$

答案：
6.D [解析] 菱形的性质+全等三角形的判定与性质+三角形的中位线定理+特殊角的三角函数值 如图，过点F作FM//AB，交DE于点M，过点C作CN⊥AB，交AB的延长线于点N，连接BF。在菱形ABCD中，AB = BC = CD = 2，AD//BC，AB//DC，
∴FM是△ECD的中位线。
∴FM = $\frac{1}{2}$DC = 1。又点E是AB的中点，
∴AE = BE = $\frac{1}{2}$AB = 1。
∴FM = AE。
∵FM//AB，
∴∠MFG = ∠GAE，∠FMG = ∠GEA(提示：两直线平行，内错角相等)。
∴△FGM≌△AGE(ASA)。
∴AG = FG。
∵AD//BC，
∴∠CBN = ∠DAB = 60°(提示：两直线平行，同位角相等)。在Rt△BCN中，BC = 2，
∴CN = BC⋅sin60° = 2×$\frac{\sqrt{3}}{2}$ = $\sqrt{3}$，BN = BC⋅cos60° = 2×$\frac{1}{2}$ = 1。
∴BE = BN = 1。
∴BF是△ECN的中位线。
∴BF//CN，BF = $\frac{1}{2}$CN = $\frac{\sqrt{3}}{2}$。
∴∠ABF = ∠BNC = 90°(提示：两直线平行，同位角相等)。在Rt△ABF中，由勾股定理可得AF = $\sqrt{AB²+BF²}$ = $\sqrt{2²+(\frac{\sqrt{3}}{2})²}$ = $\frac{\sqrt{19}}{2}$，
∴GF = $\frac{1}{2}$AF = $\frac{\sqrt{19}}{4}$，即GF的长等于$\frac{\sqrt{19}}{4}$。故选D。

1. （2025·武汉）如图1，在$\triangle ABC$中，$D$是边$AC$上的定点. 点$P$从点$A$出发，依次沿$AB$，$BC$两边匀速运动，运动到点$C$时停止. 设点$P$运动的路程为$x$，$DP$的长为$y$，$y$关于$x$的函数图象如图2所示，其中$M$，$N$分别是两段曲线的最低点. 点$N$的纵坐标是（ ）

A.$\frac{116}{17}$
B.$\frac{120}{17}$
C.$\frac{112}{15}$
D.$\frac{116}{15}$

答案：
1.B [解析] 勾股定理及其逆定理+三角形面积公式+函数图象的分析 如图，连接BD，作DH⊥AB于点H，DT⊥BC于点T。由题意及题中图象知AD = 20，BD = 15，CD = 8，DH = 12，点N的纵坐标即为DT的值。在Rt△ADH中，由勾股定理得AH = $\sqrt{AD²−DH²}$ = 16。在Rt△DHB中，由勾股定理得BH = $\sqrt{BD²−DH²}$ = 9。
∴AB = AH + BH = 25。
∵BD² + AD² = AB²，
∴BD⊥AC。
∴BC² = CD² + BD² = 8² + 15² = 17²。
∴BC = 17。由CD⋅BD = BC⋅DT得DT = $\frac{CD⋅BD}{BC}$ = $\frac{120}{17}$，即点N的纵坐标为$\frac{120}{17}$。故选B。

2. 如图1，在平行四边形$ABCD$中，$AB = 3$，$BD \perp AB$，动点$F$从点$A$出发，沿折线$ADB$以每秒$1$个单位长度的速度运动到点$B$. 图2是点$F$运动时，$\triangle FBC$的面积$y$随时间$x$变化的图象，则$m$的值为（A）

A.$6$
B.$10$
C.$12$
D.$20$

答案： 2.A [解析] 函数的图象+勾股定理 由题图可知，AD = a，AD + BD = 9，则BD = 9−a。由BD⊥AB，可得△ABD是直角三角形，则由勾股定理可得AD² = BD² + AB²，即a² = (9−a)² + 3²，解得a = 5，即AD = 5(关键：利用勾股定理求出a的值)。所以BD = 4。所以m = $S_{△BDC}$ = $\frac{1}{2}$×3×4 = 6。故选A。

3. 如图1，在平面直角坐标系中，将$□ ABCD$放置在第一象限，且$AB // x$轴. 直线$y = -x$从原点出发沿$x$轴正方向平移，在平移过程中直线被平行四边形截得的线段长度$l$与直线在$x$轴上平移的距离$m$的函数图象如图2所示，则$□ ABCD$的面积为（ ）

A.$5\sqrt{2}$
B.$5\sqrt{3}$
C.$5\sqrt{6}$
D.$10$

答案：
3.B [解析] 函数图象的分析
第1步，理解函数图象，确定关键点的意义
由题中图象可知，直线经过A时平移的距离为3，经过D时平移的距离为7，经过B时平移的距离为8，
∴AB = 5。
第2步，构造直角三角形求解线段长
如图，设当直线经过点D时，交AB于点E，过点D作DF⊥AB于点F，由题中函数图象知DE = $\sqrt{6}$，易得∠DEF = 45°，
∴DF = EF = $\sqrt{3}$。
第3步，计算面积
∴□ABCD的面积为AB⋅DF = 5×$\sqrt{3}$ = 5$\sqrt{3}$。故选B。

4. 如图1，在菱形$ABCD$中，$\angle ABC = 60^{\circ}$，连接$BD$，点$M$从$B$出发沿$BD$方向以$\sqrt{3}\ cm/s$的速度运动至$D$，同时点$N$从$B$出发沿$BC$方向以$1\ cm/s$的速度运动至$C$，设运动时间为$x(s)$，$\triangle BMN$的面积为$y(cm^2)$，$y$与$x$的函数图象如图2所示，则菱形$ABCD$的边长为（ ）

A.$2\sqrt{2}\ cm$
B.$4\sqrt{2}\ cm$
C.$4\ cm$
D.$8\ cm$

答案：
4.C [解析] 菱形的性质+解直角三角形+三角形的面积公式+从函数图象提取信息
【思维导图】过点N作NH⊥BM于点H→BN = x，BM = $\sqrt{3}$x→∠CBD = 30°→锐角三角函数→NH = $\frac{1}{2}$x→四边形ABCD是菱形→y = $S_{△BMN}$ = $\frac{\sqrt{3}}{4}$x²→解方程x→BC的长为4cm→得解。
如图，过点N作NH⊥BM于点H，由题意知，BN = x，BM = $\sqrt{3}$x。在菱形ABCD中，∠ABC = 60°，则∠CBD = 30°。在Rt△BNH中，NH = BN⋅sin30° = $\frac{1}{2}$x，
∴y = $S_{△BMN}$ = $\frac{1}{2}$⋅BM⋅NH = $\frac{\sqrt{3}}{4}$x²。当点N运动到点C时，过点C作CO⊥BD于点O，在Rt△BOC中，BC = x，
∴BO = BC⋅cos30° = $\frac{\sqrt{3}}{2}$x。
∴BD = 2BO = $\sqrt{3}$x，即此时点M运动到点D。则此时△BMN的面积最大。由图象可知，y的最大值为4$\sqrt{3}$，则y = $\frac{\sqrt{3}}{4}$x² = 4$\sqrt{3}$，解得x = 4或−4(舍去)，
∴BC的长为4cm，即菱形ABCD的边长为4cm。故选C。