《2026年天利38套中考试题精选数学浙江专版》

1. 甲、乙两个弹簧，在一定的弹性限度内，两个弹簧挂重物后可达到的最大长度均为 $ a $ 厘米。甲弹簧原长 3 厘米，每挂质量为 1 千克的重物弹簧伸长 1 厘米。两个弹簧各自的长度 $ y $（厘米）与所挂重物质量 $ x $（千克）之间的函数图象如图所示。

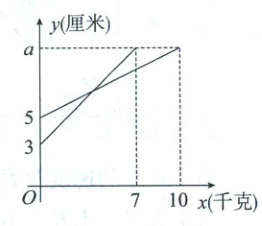
（1）求 $ a $ 的值。
（2）求乙弹簧的长度 $ y $ 与 $ x $ 之间的函数表达式，并写出自变量 $ x $ 的取值范围。
（3）在弹性限度内，把两个质量相同的重物分别挂在甲、乙两个弹簧上，发现弹簧的长度恰好相同。若把这两个重物同时挂在乙弹簧上，求此时乙弹簧的长度。

答案： （1）由题意得，$a = 7×1 + 3 = 10$.
（2）设所求函数表达式为$y = kx + b(k\neq0)$.将点$(0,5)$，$(10,10)$的坐标代入，得$\begin{cases}b = 5\\10k + b = 10\end{cases}$，解得$\begin{cases}k = 0.5\\b = 5\end{cases}$，所以$y$与$x$之间的函数表达式为$y = 0.5x + 5(0\leq x\leq10)$.
（3）根据题意，得$3 + x = 0.5x + 5$，解得$x = 4$.因为$4 + 4 = 8$(千克)，所以，当$x = 8$时，$y = 0.5×8 + 5 = 9$.
答：此时乙弹簧的长度为9厘米.

2. 随着科技的进步，传统的人工生产方式开始向自动化和智能化转变。某工厂工人每日上、下午各工作 3 小时，中间休息 2 小时。假设每名工人和每台机器人工作时的效率不变，一台机器人每日工作量 $ y_1 $（件），一名工人每日工作量 $ y_2 $（件）分别与机器人工作时间 $ x $（小时）之间的函数关系如图所示。

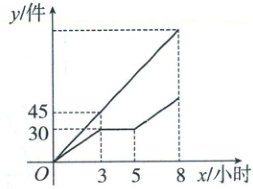
（1）求机器人的工作效率。
（2）当 $ 5 \leqslant x \leqslant 8 $ 时，求 $ y_2 $ 关于 $ x $ 的函数表达式。
（3）当 $ x = 8 $ 时，求一台机器人比一名工人多生产的产品数量。

答案： （1）由题意得，$45÷3 = 15$(件/小时)，即机器人的工作效率为15(件/小时).
（2）由题图可知，一名工人的工作效率为$\frac{30}{3}=10$(件/小时)，$\therefore$当$5\leq x\leq8$时，设$y_2$与$x$的函数表达式为$y_2 = 10x + b$，把$(5,30)$的坐标代入，得$10×5 + b = 30$，解得$b = - 20$，$\therefore y_2$与$x$的函数表达式为$y_2 = 10x - 20(5\leq x\leq8)$.
（3）当$x = 8$时，$15×8 = 120$，即一台机器人生产的产品数量是120件.$y_2 = 10×8 - 20 = 60$，即一名工人生产的产品数量是60件.$\therefore120 - 60 = 60$，$\therefore$当$x = 8$时，一台机器人比一名工人多生产产品60件.