《2026年天利38套中考试题精选数学浙江专版》

23. （本小题满分10分）甲、乙、丙三个同学研究了二次函数$y=ax^{2}-2ax+a-1(a\neq0)$的图象和性质，并交流了自己的学习成果.
（1）甲同学的说法：当$x=0$和$x=2$时，函数值相等.你认为甲同学的说法正确吗？请说明理由.
（2）乙同学的发现：$a$取某个值时，该函数图象上到$x$轴的距离为1的点有3个，且以这三个点为顶点的三角形的面积为3.根据乙同学的发现，求出此时$a$的值.
（3）丙同学的探索：若$a＞0$，当$0＜x＜3$时，$y$的取值范围中恰有4个不同的整数值.根据丙同学的结论，求出$a$的取值范围.

答案： 23. 二次函数的图象与性质
解：
(1)
∵$y = ax^2 - 2ax + a - 1 = a(x - 1)^2 - 1$，
∴抛物线的对称轴为直线$x = 1$.
∴当$x = 0$和$x = 2$时，函数值相等.
∴甲同学说法正确. (2分)
(2)解法一（三角形法）：
∵抛物线的顶点坐标为$(1, -1)$，
∴顶点到$x$轴的距离为1.
由条件可知$a ＞ 0$，三角形的另外两个顶点的纵坐标都为1，
∴题设中的三角形是高为2、底边长为3的等腰三角形.
∴底边顶点坐标分别为$(\frac{5}{2},1)$，$(-\frac{1}{2},1)$. (4分)
代入$y = a(x - 1)^2 - 1$中，得$1 = a(\frac{5}{2} - 1)^2 - 1$，
解得$a = \frac{8}{9}$. (6分)
解法二（两点距离法）：$a$取某个值时，该函数图象上到$x$轴的距离为1的点有3个，则这三个点有一个是顶点，则三角形的高为2，由抛物线的表达式知，其顶点坐标为$(1, -1)$，则$a ＞ 0$.
令$y = ax^2 - 2ax + a - 1 = 1$，解得$x = 1 \pm \sqrt{\frac{2}{a}}$
则两个点之间的距离为$2\sqrt{\frac{2}{a}}$，
则$\frac{1}{2} × (2\sqrt{\frac{2}{a}}) × 2 = 3$，则$a = \frac{8}{9}$. (6分)
(3)
∵$a ＞ 0$，抛物线的顶点坐标为$(1, -1)$，
∴当$0 ＜ x ＜ 3$时，$-1 \leqslant y ＜ 4a - 1$. (8分)
∴4个不同的整数值分别为$-1,0,1,2$，即$2 ＜ 4a - 1 \leqslant 3$.
∴$\frac{3}{4} ＜ a \leqslant 1$. (10分)

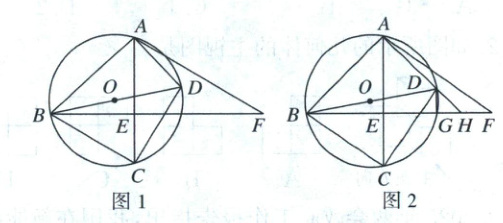
24. （本小题满分12分）如图1，四边形$ABCD$内接于$\odot O$，$BD$为直径，$∠ABC$为锐角，过点$B$作$BE\perp AC$于点$E$，过点$A$作$BC$的平行线交$BE$的延长线于点$F$.
（1）若$∠ABD=\alpha$，请用含$\alpha$的代数式表示$∠CBE$.
（2）若$AF=BD$，求证：$AD=AE$.
（3）如图2，在（2）的条件下，$BF$与$\odot O$交于点$G$，与$AD$的延长线交于点$H$，连接$DG$.
①若$CD=4$，$DG=1$，求$AD$的长.
②若$\cos∠AHB=\frac{DG}{HF}$，求$\tan∠ABD$的值.

答案：
24. 圆的综合题
解：
(1)
∵$BD$为直径，
∴$\angle BCD = 90°$.
∵$\angle ABD = \angle ACD = \alpha$，
∴$\angle ACB = 90° - \alpha$.
∵$BE \perp AC$于点$E$，
∴$\angle CBE = \alpha$. (3分)
(2)证明：
∵$AF // BC$，
∴$\angle AFE = \angle CBE = \angle ABD$.
∵$\angle BAD = \angle FEA = 90°$，$AF = BD$，
∴$\triangle ABD \cong \triangle EFA$（AAS）.
∴$AD = AE$. (6分)
(3)①[第1步，利用圆周角定理的推论和等弧对等弦的性质得$AG,CD$的关系]
连接$AG$，作$DM \perp AC$于点$M$，如图1（巧作辅助线：作垂直，构造矩形，进而运用矩形的性质求解），

由
(2)知，$\angle CBE = \angle ABD$.
∵$\angle CAG = \angle CBE$，$\angle ACD = \angle ABD$，
∴$\angle ACD = \angle CAG$.
∴$AD = CG$.
∴$\overset{\frown}{AG} = \overset{\frown}{AD} + \overset{\frown}{DG} = \overset{\frown}{CG} + \overset{\frown}{DG} = \overset{\frown}{CD}$.
∴$AG = CD = 4$（提示：在同圆或等圆中，等弧对等弦）.
[第2步，利用矩形的判定与性质得到$ME = DG$，$DM = EG$]
∵$BD$为直径，
∴$DG \perp BG$.
∵$BG \perp AE$，
∴四边形$DGEM$为矩形.
∴$ME = DG = 1$，$DM = EG$.
[第3步，利用勾股定理求出$AD$的长度]
设$AD = AE = x$，则$AM = x - 1$.
∵$EG^2 = AG^2 - AE^2$，$DM^2 = AD^2 - AM^2$.
∴$16 - x^2 = x^2 - (x - 1)^2$，
解得$x_1 = 3\sqrt{2} - 1$，$x_2 = -3\sqrt{2} - 1$（舍去）.
∴$AD$的长为$3\sqrt{2} - 1$. (9分)
②[第1步，利用圆周角定理的推论及三角函数的定义得到$\frac{DC}{BD} = \frac{AG}{AF}$]
连接$AG$，如图2.（巧作辅助线：连接$AG$，构造出符合圆周角定理的推论的条件），

∵$BD$为直径，
∴$\angle BAH = 90°$.
∴$\angle AHB + \angle ABH = 90°$.
∵$AE \perp BE$，
∴$\angle BAC + \angle ABH = 90°$.
∴$\angle AHB = \angle BAC = \angle BDC$.
∵$AG = CD$，$BD = AF$，
∴$\cos \angle BDC = \frac{DC}{BD} = \frac{AG}{AF}$.
[第2步，用相似三角形的判定与性质得到$\angle ADG = \angle AHF$]
∵$\cos \angle AHB = \frac{DG}{HF}$，
∴$\frac{DG}{HF} = \frac{AG}{AF}$.
又
∵$\triangle ABD \cong \triangle EFA$（AAS），
∴$\angle AFH = \angle ABD = \angle AGD$.
∴$\triangle AGD \sim \triangle AFH$.
∴$\angle ADG = \angle AHF$.
[第3步，根据等腰直角三角形的性质和三角函数的定义求解]
∵$DG \perp BF$，
∴$\angle GDH = \angle DHG = 45°$.
∵$\angle BAD = 90°$，
∴$AB = \sqrt{2}AE = \sqrt{2}AD$.
∴$\tan \angle ABD = \frac{\sqrt{2}}{2}$. (12分)
（解析人：全应毅）