第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 比$-1$大2的数为(
A.$-3$
B.0
C.1
D.2
C
)A.$-3$
B.0
C.1
D.2
答案:
1. C 【考点】有理数的加法运算
2. 如图所示的几何体的主视图是(
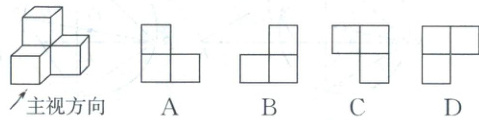
A
)
答案:
2. A 【考点】三视图
3. 2025年两会政府工作报告指出,我国在新能源汽车产业研发领域投入资金24970000000元.其中数24970000000用科学记数法表示为(
A.$2.497×10^{8}$
B.$2.497×10^{9}$
C.$24.97×10^{9}$
D.$2.497×10^{10}$
D
)A.$2.497×10^{8}$
B.$2.497×10^{9}$
C.$24.97×10^{9}$
D.$2.497×10^{10}$
答案:
3. D 【考点】科学记数法表示较大的数
4. 下列运算正确的是(
A.$a^{2}+a^{3}=a^{5}$
B.$a^{2}·a^{3}=a^{6}$
C.$(3a)^{2}=6a^{2}$
D.$a^{5}÷a^{3}=a^{2}$
D
)A.$a^{2}+a^{3}=a^{5}$
B.$a^{2}·a^{3}=a^{6}$
C.$(3a)^{2}=6a^{2}$
D.$a^{5}÷a^{3}=a^{2}$
答案:
4. D 【解析】同类项+同底数幂的乘法+积的乘方+同底数幂的除法
选项 逐项分析 正误
A $a^2$与$a^3$不属于同类项,不能合并 $×$
B $a^2 · a^3 = a^5$ $×$
C $(3a)^2 = 9a^2$ $×$
D $a^5 ÷ a^3 = a^2$ $\surd$
故选D.
选项 逐项分析 正误
A $a^2$与$a^3$不属于同类项,不能合并 $×$
B $a^2 · a^3 = a^5$ $×$
C $(3a)^2 = 9a^2$ $×$
D $a^5 ÷ a^3 = a^2$ $\surd$
故选D.
5. 若关于$x$的一元二次方程$x^{2}-2x+k-1=0$有两个相等的实数根,则$k$的值为(
A.$k=2$
B.$k=0$
C.$k=-1$
D.$k=-2$
A
)A.$k=2$
B.$k=0$
C.$k=-1$
D.$k=-2$
答案:
5. A 【解析】一元二次方程根的判别式
∵关于$x$的一元二次方程$x^2 - 2x + k - 1 = 0$有两个相等的实数根,
∴$\Delta = (-2)^2 - 4(k - 1) = 0$,解得$k = 2$. 故选A.
∵关于$x$的一元二次方程$x^2 - 2x + k - 1 = 0$有两个相等的实数根,
∴$\Delta = (-2)^2 - 4(k - 1) = 0$,解得$k = 2$. 故选A.
6. 图1是阿基米德的滑动曲尺模型,图2是其抽象成的几何图形.$AB$为$\odot O$的直径,其延长线与弦$DC$的延长线交于点$E$,$CE=CO$.若$∠AOD=60^{\circ}$,则$∠AED$的度数为(
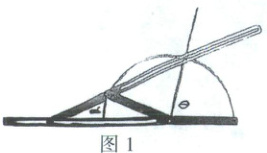
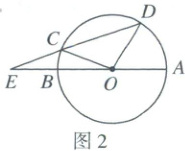
A.$15^{\circ}$
B.$20^{\circ}$
C.$25^{\circ}$
D.$30^{\circ}$
B
)

A.$15^{\circ}$
B.$20^{\circ}$
C.$25^{\circ}$
D.$30^{\circ}$
答案:
6. B 【解析】等腰三角形的性质+三角形外角的性质
∵$CE = CO$,
∴$\angle AED = \angle COE$.
∵$CO = DO$,
∴$\angle OCD = \angle D$.
∵$\angle OCD = \angle AED + \angle COE$,
∴$\angle D = \angle OCD = 2\angle AED$.
∵$\angle AOD = \angle AED + \angle D = 60°$,
∴$\angle AED = 20°$. 故选B.
∵$CE = CO$,
∴$\angle AED = \angle COE$.
∵$CO = DO$,
∴$\angle OCD = \angle D$.
∵$\angle OCD = \angle AED + \angle COE$,
∴$\angle D = \angle OCD = 2\angle AED$.
∵$\angle AOD = \angle AED + \angle D = 60°$,
∴$\angle AED = 20°$. 故选B.
7. 已知$A(x_{1},y_{1})$,$B(x_{2},y_{2})$,$C(x_{3},y_{3})$是反比例函数$y=\frac{-5}{x}$图象上的三个点,若$x_{1}<x_{2}<0<x_{3}$,则$y_{1}$,$y_{2}$,$y_{3}$的大小关系为(
A.$y_{1}<y_{2}<y_{3}$
B.$y_{2}<y_{1}<y_{3}$
C.$y_{3}<y_{2}<y_{1}$
D.$y_{3}<y_{1}<y_{2}$
D
)A.$y_{1}<y_{2}<y_{3}$
B.$y_{2}<y_{1}<y_{3}$
C.$y_{3}<y_{2}<y_{1}$
D.$y_{3}<y_{1}<y_{2}$
答案:
7. D 【解析】反比例函数的图象与性质
∵反比例函数$y = \frac{-5}{x}$中,$k = -5 < 0$,
∴此函数图象在第二、四象限,在每个象限内$y$随$x$的增大而增大.
∵$A(x_1,y_1)$,$B(x_2,y_2)$,$C(x_3,y_3)$是反比例函数$y = \frac{-5}{x}$图象上的三个点,且$x_1 < x_2 < 0 < x_3$,
∴点$C(x_3,y_3)$在第四象限,则$y_3 < 0$. 点$A(x_1,y_1)$,$B(x_2,y_2)$在第二象限,则$y_2 > y_1 > 0$,
∴$y_3 < y_1 < y_2$. 故选D.
∵反比例函数$y = \frac{-5}{x}$中,$k = -5 < 0$,
∴此函数图象在第二、四象限,在每个象限内$y$随$x$的增大而增大.
∵$A(x_1,y_1)$,$B(x_2,y_2)$,$C(x_3,y_3)$是反比例函数$y = \frac{-5}{x}$图象上的三个点,且$x_1 < x_2 < 0 < x_3$,
∴点$C(x_3,y_3)$在第四象限,则$y_3 < 0$. 点$A(x_1,y_1)$,$B(x_2,y_2)$在第二象限,则$y_2 > y_1 > 0$,
∴$y_3 < y_1 < y_2$. 故选D.
8. 在一次体育测试中,某班40名学生的跳绳成绩(单位:次)如表所示:
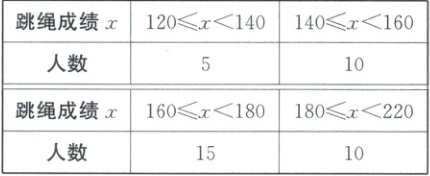
则下列关于这40名学生跳绳成绩的统计量,说法正确的是(
A.平均数一定是170
B.众数一定是170
C.中位数在160~180范围内(含160,不含180)
D.方差为0

则下列关于这40名学生跳绳成绩的统计量,说法正确的是(
C
)A.平均数一定是170
B.众数一定是170
C.中位数在160~180范围内(含160,不含180)
D.方差为0
答案:
8. C 【解析】平均数+方差+中位数+众数 选项A,B,D均不能确定,故A,B,D不符合题意. 中位数在$160 \sim 180$范围内(含$160$,不含$180$),故C符合题意. 故选C.
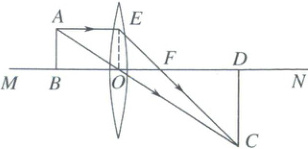
9. 如图是凸透镜成像的光路示意图,$AB$,$CD$,$OE$分别表示蜡烛、蜡像、凸透镜,它们均与主光轴$MN$垂直.一束平行于主光轴的光线$AE$经凸透镜折射后,其折射光线经过焦点$F$,一束经过光心的光线$AO$与折射光线$EF$相交于点$C$.已知$OF=10cm$,$OB=15cm$,则$\frac{CD}{AB}$的值为(
A.$\frac{2}{3}$
B.$\frac{3}{2}$
C.2
D.$\frac{5}{2}$
2
)
A.$\frac{2}{3}$
B.$\frac{3}{2}$
C.2
D.$\frac{5}{2}$
答案:
9. C 【解析】相似三角形的判定与性质+矩形的性质 根据题意可得$\triangle EOF \sim \triangle CDF$,$\triangle ABO \sim \triangle CDO$,
∴$\frac{CD}{EO} = \frac{DF}{OF}$,$\frac{CD}{AB} = \frac{OD}{OB}$. 易知四边形ABOE是矩形,
∴$OE = AB$,即$\frac{DF}{10} = \frac{10 + FD}{15}$,解得$DF = 20 cm$.
∴$\frac{CD}{AB} = \frac{OD}{OB} = \frac{10 + 20}{15} = 2$. 故选C.
∴$\frac{CD}{EO} = \frac{DF}{OF}$,$\frac{CD}{AB} = \frac{OD}{OB}$. 易知四边形ABOE是矩形,
∴$OE = AB$,即$\frac{DF}{10} = \frac{10 + FD}{15}$,解得$DF = 20 cm$.
∴$\frac{CD}{AB} = \frac{OD}{OB} = \frac{10 + 20}{15} = 2$. 故选C.
查看更多完整答案,请扫码查看


