《2026年天利38套中考试题精选数学浙江专版》

10. 已知$\triangle ABC$中，$AB^{2}=AC(AC+BC)$，则（ ）

A.$∠ABC=2∠ACB$
B.$∠ACB=2∠ABC$
C.$∠ACB=2∠BAC$
D.$∠BAC=2∠ABC$

答案：
10. B　[解析]相似三角形的判定与性质　如图，延长$AC$到点$D$，使$CD = BC$，连接$BD$，$\therefore \angle D = \angle CBD$. $\therefore \angle ACB = \angle D + \angle CBD = 2\angle D$.
∵$AB^2 = AC(AC + BC)$，$\therefore AB^2 = AC · AD$. $\therefore \frac{AB}{AC} = \frac{AD}{AB}$.
∵$\angle BAC = \angle BAD$，$\therefore \triangle ABC \sim \triangle ADB$. $\therefore \angle ABC = \angle D$. $\therefore \angle ACB = 2\angle ABC$.故选B.
　　　　　　　　

11. 因式分解：$4x^{2}-y^{2}=$$(2x + y)(2x - y)$.

答案： 11. $(2x + y)(2x - y)$　[考点]因式分解

12. 若二次根式$\sqrt{2-a}$有意义，则$a$的取值范围为$a \leq 2$.

答案： 12. $a \leq 2$　[解析]二次根式成立的条件　由题意知，$2 - a \geq 0$，解得$a \leq 2$(易错:当不等式两边同时除以负数时，不等号的开口方向要改变).

13. 一个不透明的袋子中有4个白球，2个红球和$a$个黑球，它们除颜色外其余都相同.从中随机摸一个球，摸到黑球的概率为$\frac{2}{5}$，则$a$的值为4.

答案： 13. 4　[解析]概率　由题意可得，$\frac{a}{4 + 2 + a} = \frac{2}{5}$，解得$a = 4$.经检验，$a = 4$是原分式方程的解，$\therefore a$的值为4.

14. 如图，$PA$，$PB$为$\odot O$的两条切线，点$A$，$B$为切点，点$C$在劣弧$AB$上.若$∠ACB=115^{\circ}$，则$∠P$的度数为__________.

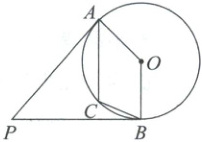
50°

答案： 14. $50°$　[解析]圆周角定理+四边形的内角和+圆的切线的性质
∵$\angle ACB = 115°$，优弧$AB$所对的圆心角度数为$2 × 115° = 230°$(提示:同弧所对的圆周角等于所对圆心角的一半). $\therefore \angle AOB = 360° - 230° = 130°$.又
∵$PA$，$PB$是$\odot O$的切线，$\therefore \angle PAO = \angle PBO = 90°$(提示:圆的切线垂直于过切点的半径). $\therefore \angle P = 360° - 90° - 90° - 130° = 50°$，即$\angle P$的度数为$50°$.

15. 如图，款式相同的4个碗叠放在一起总高度为11.5cm，若同款的7个碗叠放在一起总高度为16cm，则一个碗的高度为7cm.

答案： 15. 7　[解析]二元一次方程组的应用　根据题意，设一个碗的高度为$x cm$，每叠一个碗增加的高度为$y cm$，$\begin{cases}x + 3y = 11.5 \\x + 6y = 16\end{cases}$，解得$\begin{cases}x = 7 \\y = 1.5\end{cases}$.因此一个碗的高度为$7 cm$.

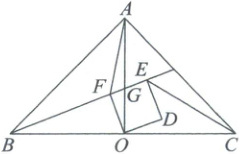
16. 如图，在$\triangle ABC$中，$∠BAC=90^{\circ}$，$AB=AC$，点$O$为$BC$中点，连接$AO$，正方形$ODEF$在$\triangle ABC$内部，边$EF$交$AO$于点$G$，连接$AF$，$CE$.若点$G$为$EF$中点，$AF=\sqrt{17}$，$EF=\sqrt{5}$，则线段$CE$的长为______.

答案：
16. $\sqrt{34}$　[解析]　等腰直角三角形的性质+正方形的性质+全等三角形的判定与性质+平行四边形的判定与性质+勾股定理+相似三角形的判定与性质
[第1步，作$DN \perp BC$，$EM \perp BC$，$EM$交$OD$于点$P$，利用等腰直角三角形和正方形的性质证三角形全等，得$CD$的长]如图，连接$CD$，过点$D$作$DN \perp BC$于点$N$，过点$E$作$EM \perp BC$于点$M$，$EM$交$OD$于点$P$(巧作辅助线:构造直角三角形及平行线).在$\triangle ABC$中，$\angle BAC = 90°$，$AB = AC$，点$O$为$BC$的中点，$\therefore OA = OB = OC = \frac{1}{2}BC$，$\angle AOB = \angle AOC = 90°$.
∵四边形$ODEF$是正方形，且$EF = \sqrt{5}$，$\therefore OF = OD = DE = EF = \sqrt{5}$，$\angle OFE = \angle DOF = \angle ODE = 90°$，$EF // OD$.
∵$\angle AOC = \angle DOF = 90°$，$\therefore \angle AOF + \angle AOD = \angle AOD + \angle COD = 90°$. $\therefore \angle AOF = \angle COD$.又$OA = OC$，$OF = OD$，$\therefore \triangle AOF \cong \triangle COD (SAS)$. $\therefore CD = AF = \sqrt{17}$.
[第2步，证明四边形$EGOP$是平行四边形，利用相似三角形和勾股定理求$ON$，$CN$的长]
∵点$G$为$EF$的中点，$\therefore EG = FG = \frac{1}{2}EF = \frac{\sqrt{5}}{2}$.
∵$\angle AOC = \angle EMC = 90°$，$\therefore AO // EM$.又$EF // OD$，四边形$EGOP$是平行四边形(提示:两组对边分别平行的四边形是平行四边形). $\therefore OP = EG = \frac{\sqrt{5}}{2}$，$OG = EP$. $\therefore DP = OD - OP = \sqrt{5} - \frac{\sqrt{5}}{2} = \frac{\sqrt{5}}{2}$.在$Rt \triangle DEP$中，由勾股定理可得$EP = \sqrt{DE^2 + DP^2} = \sqrt{(\sqrt{5})^2 + (\frac{\sqrt{5}}{2})^2} = \frac{5}{2}$，$\therefore OG = EP = \frac{5}{2}$.
∵$\angle FOG = \angle DON$，$\angle OFG = \angle OND = 90°$，$\therefore \triangle FOG \sim \triangle NOD$. $\therefore \frac{FG}{ND} = \frac{OG}{OD}$，即$\frac{\frac{\sqrt{5}}{2}}{ND} = \frac{\frac{5}{2}}{\sqrt{5}}$，解得$ND = 1$.在$Rt \triangle ODN$中，由勾股定理可得$ON = \sqrt{OD^2 - ND^2} = \sqrt{(\sqrt{5})^2 - 1^2} = 2$.在$Rt \triangle CDN$中，由勾股定理可得$CN = \sqrt{CD^2 - DN^2} = \sqrt{(\sqrt{17})^2 - 1^2} = 4$.
[第3步，利用平行线的判定、平行线分线段成比例定理、三角形中位线定理及勾股定理求出$CE$的长]
∵$EM \perp BC$，$DN \perp BC$，$\therefore EM // DN$.
∵$OP = PD = \frac{\sqrt{5}}{2}$，$\therefore OM = MN = \frac{1}{2}ON = 1$. $\therefore PM = \frac{1}{2}DN = \frac{1}{2}$. $\therefore CM = CN + MN = 4 + 1 = 5$，$EM = EP + PM = \frac{5}{2} + \frac{1}{2} = 3$.在$Rt \triangle CEM$中，由勾股定理可得$CE = \sqrt{EM^2 + CM^2} = \sqrt{3^2 + 5^2} = \sqrt{34}$，即$CE$的长为$\sqrt{34}$.
　　　　　　　　

17. （本小题满分8分）计算：（1）$|-4|-(-3)^{2}×2$.
（2）$\frac{1}{x - 1}-\frac{x}{x - 1}$.

答案： 17. 实数的运算+分式的运算
解:
(1)原式$= 4 - 9 × 2 = 4 - 18 = -14$.　　　　　　　　(4分)
(2)原式$= \frac{1 - x}{x - 1} = -1$.　　　　　　　　　　　　　　　(4分)

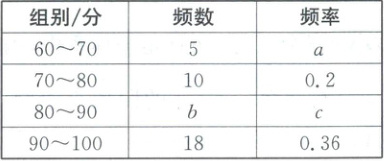
18. （本小题满分8分）某中学举行“垃圾分类投放和分类处理”知识竞赛，随机抽取部分学生的成绩进行统计，并绘制成如图所示的未完成的频数表与频数分布直方图（每一组不含前一个边界值，含后一个边界值）.
抽取的学生的成绩频数表


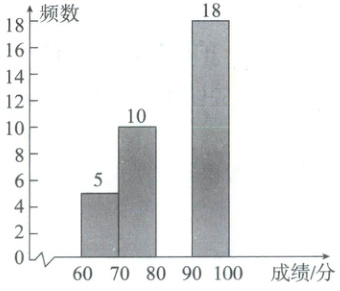
抽取的学生的成绩频数分布直方图
请根据所给信息，解答下列问题：
（1）填空：$a=$______，$b=$______，$c=$______.
（2）补全频数分布直方图.
（3）若成绩在80分以上为优秀，请你根据抽取的

样

本

数

据，估计参加这次比赛的800名学生中成绩优秀的学生约有多少名.

答案：
18. 统计图表的应用+用样本估计总体
解:
(1)$0.1$　17　$0.34$.　　　　　　　　　　　　　　　(3分)
[解题过程]
∵$10 ÷ 0.2 = 50$，即共抽取了50名学生的成绩，$\therefore a = 5 ÷ 50 = 0.1$，$b = 50 - 5 - 10 - 18 = 17$. $\therefore c = 17 ÷ 50 = 0.34$.
(2)补全频数分布直方图如图所示.
　　　　　
(3)$800 × \frac{17 + 18}{50} = 560$(名).
答:估计参加这次比赛的800名学生中成绩优秀的学生约有560名.　　　　　　　　　　　　　　　　　　　　　　(8分)