《2026年天利38套中考试题精选数学浙江专版》

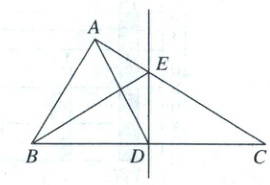
20. (本小题满分 8 分)如图,在$Rt\triangle ABC$中,$\angle BAC=90^{\circ},BC$边上的垂直平分线分别交$BC,AC$于点$D$和点$E$,连接$AD,BE$.
(1)求证:$\angle ADB=2\angle EBD$.
(2)若$BC=8,DE=3$,求$AE$的长度.

答案： 20. 直角三角形的性质+线段垂直平分线的性质+相似三角形的判定与性质+三角形的外角性质
解：
(1)证明：$\because \angle BAC = 90^{\circ}$,$D$为$BC$中点，
$\therefore AD = CD$(提示：直角三角形斜边上的中线等于斜边的一半).
$\therefore \angle DAC = \angle C$.
$\therefore \angle ADB = \angle DAC + \angle C = \angle C + \angle C = 2\angle C$.
$\because DE$为$BC$的垂直平分线，
$\therefore BE = CE$(提示：线段垂直平分线上的点到线段两端点的距离相等).
$\therefore \angle C = \angle EBD$.
$\therefore \angle ADB = 2\angle EBD$.
(2)$\because DE$为$BC$的垂直平分线，$BC = 8$,
$\therefore BD = CD = 4$,$\angle EDC = 90^{\circ}$.
$\because \angle BAC = \angle EDC = 90^{\circ}$.
$\because DE = 3$,
$\therefore BE = CE = 5$.
$\because \angle C = \angle C$,
$\therefore \triangle EDC \sim \triangle BAC$.
$\therefore \frac{DC}{AC} = \frac{CE}{CB}$,即$\frac{4}{AC} = \frac{5}{8}$.
$\therefore AC = \frac{32}{5}$.
$\therefore AE = \frac{7}{5}$.

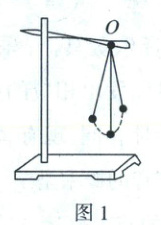
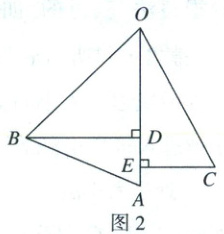
21. (本小题满分 8 分)单摆是一种能够产生往复摆动的装置. 如图 1,在支架的横杆点$O$处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动(摆线的长度变化忽略不计). 如图 2,摆球静止时的位置为点$A$,拉紧摆线将摆球拉至点$B$处,过点$B$作$BD\perp OA$于点$D$. 当摆球运动至点$C$时,过点$C$作$CE\perp OA$于点$E$. (点$O,A,B,C,D,E$在同一平面内)
(1)若$BD=8 cm,AD=4 cm$,求$OB$的长.
(2)若$\angle BOA=46^{\circ},\angle AOC=28^{\circ},ED=10 cm$,求$OA$的长.
($\sin 46^{\circ}\approx 0.72,\cos 46^{\circ}\approx 0.69,\tan 46^{\circ}\approx 1.04,\sin 28^{\circ}\approx 0.47,\cos 28^{\circ}\approx 0.88,\tan 28^{\circ}\approx 0.53$,结果精确到$0.1 cm$)

答案： 21. 解直角三角形的应用
解：
(1)设$OD = x$,则$OB = OA = x + 4$.
在$Rt \triangle OBD$中，$OB^{2} = BD^{2} + OD^{2}$,
$\therefore (x + 4)^{2} = 8^{2} + x^{2}$.
$\therefore x = 6$.
$\therefore OB = 10 cm$.
(2)由题知$OB = OC = OA$.
在$Rt \triangle BOD$中，$\cos \angle BOD = \cos 46^{\circ} = \frac{OD}{OB} \approx 0.69$,$\therefore OD \approx 0.69OB$.
在$Rt \triangle OEC$中，$\cos \angle EOC = \cos 28^{\circ} = \frac{OE}{OC} \approx 0.88$,$\therefore OE \approx 0.88OC$.
$\therefore ED = OE - OD = 0.19OB$.
$\because ED = 10$,$\therefore OA = OB \approx 52.6 cm$.

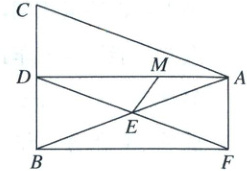
22. (本小题满分 10 分)如图,在$\triangle ABC$中,$AB=AC,D,E$分别为$BC,AB$的中点,连接$DE$并延长,使$DE=EF$.
(1)求证:四边形$ADBF$为矩形.
(2)记$\angle ADE=\alpha,\angle AEM=\beta$.
①求$\angle DEM$(用含$\alpha,\beta$的代数式表示).
②若$\beta=90^{\circ}-2\alpha$,求证:$2DE^{2}=DM· DA$.

答案： 22. 矩形的判定与性质+等腰三角形的性质+三角形内角和定理+相似三角形的判定与性质
解：
(1)证明：$\because$在$\triangle ABC$中，$AB = AC$，且$D$为$BC$的中点，
$\therefore AD \perp BD$(提示：等腰三角形“三线合一”的性质).
$\therefore \angle ADB = 90^{\circ}$.
在$Rt \triangle ABD$中，$\because E$为$AB$中点，
$\therefore DE = AE = BE$.
又$\because DE = EF$,
$\therefore$四边形$ADBF$为平行四边形.
又$\because \angle ADB = 90^{\circ}$,
$\therefore □ ADBF$为矩形.
(2)①$\because$四边形$ADBF$为矩形，
$\therefore AE = DE$.
$\therefore \angle MAE = \angle ADE = \alpha$.
又$\because \angle AEM = \beta$,
$\therefore \angle DME = \angle MAE + \angle AEM = \alpha + \beta$.
$\therefore \angle DEM = 180^{\circ} - \angle DME - \angle ADE = 180^{\circ} - 2\alpha - \beta$.
②证明：易知$\angle DAF = 90^{\circ}$,$DF = 2DE$.
$\because \beta = 90^{\circ} - 2\alpha$,
$\therefore \angle DEM = 180^{\circ} - 2\alpha - \beta = 90^{\circ}$.
$\therefore \angle DEM = \angle DAF$.
又$\because \angle MDE = \angle FDA$,
$\therefore \triangle DEM \sim \triangle DAF$.
$\because \frac{DF}{DM} = \frac{DA}{DE}$,
$\therefore DM · DA = DE · DF$,
即$DM · DA = DE · 2DE$.
$\therefore 2DE^{2} = DM · DA$.