《2025年名校课堂七年级数学上册北师大版甘肃专版》

如果两个数，它们的符号不同，数量相等，我们称其中一个数为另一个数的相反数，也称这两个数互为相反数. 特别地，0 的相反数是0.

答案： 相反数，0

1. (2023·兰州) $-5$ 的相反数是 (B)

A.$-5$
B.$5$
C.$\frac{1}{5}$
D.$-\frac{1}{5}$

答案： 1.B

2. 下列各组数中，互为相反数的是 (B)

A.$-\frac{1}{3}$ 和 $-3$
B.$-2$ 和 $2$
C.$-3.5$ 和 $5.3$
D.$\frac{3}{5}$ 和 $\frac{5}{3}$

答案： 2.B

3. 若一个数的相反数等于它本身，则这个数是 (C)

A.正数
B.负数
C.$0$
D.非负数

答案： 3.C

4. 求下列各数的相反数.
$-\frac{3}{4}$，$-0.2$，$9.2$，$0$，$4\frac{1}{3}$.

答案： 4.解：$- \frac {3}{4}，$-0.2，9.2，0，$4\frac {1}{3}$的相反数分别是$\frac {3}{4}，$0.2，-9.2，0，$-4\frac {1}{3}$

5. $-(+3)$ 表示+3(或3)的相反数，即 $-(+3)=$-3；$-(-3)$ 表示-3的相反数，即 $-(-3)=$3.

答案： 5.+3(或3) -3 -3 3

6. (2023·广州) 计算：$-(-2023)=$ (B)

A.$-2023$
B.$2023$
C.$-\frac{1}{2023}$
D.$\frac{1}{2023}$

答案： 6.B

7. 化简：
(1) $+(-8)$. (2) $-(+2.7)$.
(3) $-(-5)$. (4) $-(-\frac{3}{4})$.

答案： 7.解：
(1)原式= -8.
(2)原式= -2.7.
(3)原式= 5.
(4)原式$= \frac {3}{4}.$

8. 若 $-(+a)=+(-6)$，则 $a$ 的值是 (C)

A.$\frac{1}{6}$
B.$-\frac{1}{6}$
C.$6$
D.$-6$

答案： 8.C

9. 若 $2m + 1$ 的相反数为 $-9$，则 $m$ 的值为4.

答案： 9.4

10. 下列说法正确的有 (B)
① $3.14$ 的相反数是 $-3.14$；② 符号相反的数互为相反数；③ $-(-3.8)$ 的相反数是 $3.8$；④ 一个数和它的相反数不可能相等；⑤ 带负号的数是负数.

A.$0$ 个
B.$1$ 个
C.$2$ 个
D.$3$ 个

答案： 10.B

11. (1) 化简下列各数：
① $- [ - ( + 1 ) ]$. ② $- [ - ( - 1 ) ]$.
③ $- \{ - [ - ( + 1 ) ] \}$. ④ $- \{ - [ - ( - 1 ) ] \}$.
(2) 若化简的数不为 $0$，则化简过程中发现：化简结果的符号与原式中“$-$”的个数有着密切联系，当“$-$”的个数是奇数时，化简结果为负数；当“$-$”的个数是偶数时，化简结果为正数.

答案： 11.解：
(1)①原式= 1.②原式= -1.③原式= -1.④原式= 1.
(2)负 正

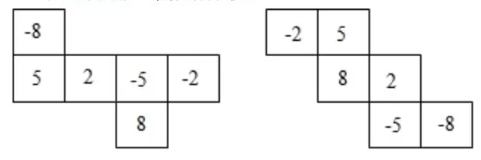
12. 如图，这是一个正方体纸盒的两个表面展开图，请把 $-8$，$5$，$8$，$-2$，$-5$，$2$ 分别填入六个正方形中，使得折成正方体后，相对面上的两个数互为相反数.

答案：
12.