第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
5. 从某多边形的一个顶点出发的所有对角线,将其分成6个三角形,则多边形的边数为(
A.6
B.7
C.8
D.9
C
)A.6
B.7
C.8
D.9
答案:
解:设多边形的边数为$n$。
从$n$边形的一个顶点出发可引$(n - 3)$条对角线,将多边形分成$(n - 2)$个三角形。
已知分成$6$个三角形,所以$n - 2 = 6$,解得$n = 8$。
答案:C
从$n$边形的一个顶点出发可引$(n - 3)$条对角线,将多边形分成$(n - 2)$个三角形。
已知分成$6$个三角形,所以$n - 2 = 6$,解得$n = 8$。
答案:C
6. 如图,若AB//CD,则∠B,∠C,∠E三者之间的关系是(
A.∠B+∠C+∠E= 180°
B.∠B+∠E-∠C= 180°
C.∠B+∠C-∠E= 180°
D.∠C+∠E-∠B= 180°
B
)A.∠B+∠C+∠E= 180°
B.∠B+∠E-∠C= 180°
C.∠B+∠C-∠E= 180°
D.∠C+∠E-∠B= 180°
答案:
解:过点E作EF//AB。
∵AB//CD,
∴EF//CD。
∵EF//AB,
∴∠B+∠BEF=180°(两直线平行,同旁内角互补)。
∵EF//CD,
∴∠FEC=∠C(两直线平行,内错角相等)。
∵∠BEF=∠BEC-∠FEC=∠E-∠C,
∴∠B+(∠E-∠C)=180°,即∠B+∠E-∠C=180°。
答案:B
∵AB//CD,
∴EF//CD。
∵EF//AB,
∴∠B+∠BEF=180°(两直线平行,同旁内角互补)。
∵EF//CD,
∴∠FEC=∠C(两直线平行,内错角相等)。
∵∠BEF=∠BEC-∠FEC=∠E-∠C,
∴∠B+(∠E-∠C)=180°,即∠B+∠E-∠C=180°。
答案:B
7. 当光线从空气射入水中时,光线的传播方向发生了改变(如图),这就是光的折射现象.若∠1= 82°,∠2= 39°,则∠3的度数为(
A.39°
B.40°
C.43°
D.45°
C
)A.39°
B.40°
C.43°
D.45°
答案:
【解析】:本题可根据平角的定义来求解$\angle3$的度数。
平角的度数为$180^{\circ}$,由图可知$\angle1$、$\angle2$与$\angle3$组成一个平角,即$\angle1 + \angle2 + \angle3 = 180^{\circ}$。
已知$\angle1 = 82^{\circ}$,$\angle2 = 39^{\circ}$,将其代入上式即可求出$\angle3$的度数。
【答案】:解:
∵$\angle1 + \angle2 + \angle3 = 180^{\circ}$,$\angle1 = 82^{\circ}$,$\angle2 = 39^{\circ}$
∴$\angle3 = 180^{\circ} - \angle1 - \angle2 = 180^{\circ} - 82^{\circ} - 39^{\circ} = 43^{\circ}- 1^{\circ}= 43^{\circ}-1^{\circ}=41^{\circ}+2^{\circ}=43^{\circ}$
所以本题选C。
平角的度数为$180^{\circ}$,由图可知$\angle1$、$\angle2$与$\angle3$组成一个平角,即$\angle1 + \angle2 + \angle3 = 180^{\circ}$。
已知$\angle1 = 82^{\circ}$,$\angle2 = 39^{\circ}$,将其代入上式即可求出$\angle3$的度数。
【答案】:解:
∵$\angle1 + \angle2 + \angle3 = 180^{\circ}$,$\angle1 = 82^{\circ}$,$\angle2 = 39^{\circ}$
∴$\angle3 = 180^{\circ} - \angle1 - \angle2 = 180^{\circ} - 82^{\circ} - 39^{\circ} = 43^{\circ}- 1^{\circ}= 43^{\circ}-1^{\circ}=41^{\circ}+2^{\circ}=43^{\circ}$
所以本题选C。
8. 完美五边形是指可以无重叠、无间隙铺满整个平面的凸五边形.如图,五边形ABCDE是迄今为止人类发现的第15种完美五边形的示意图,其中∠5= 35°,则∠1+∠2+∠3+∠4的度数为(
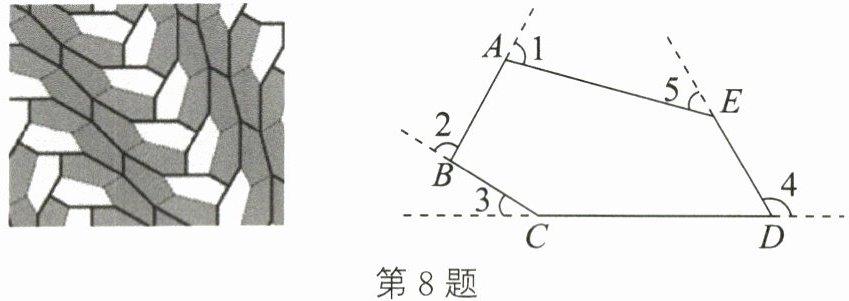
A.180°
B.360°
C.325°
D.145°
C
)
A.180°
B.360°
C.325°
D.145°
答案:
解:因为完美五边形可以无重叠、无间隙铺满整个平面,所以在平面内围绕一点的各个角的和为360°。由图可知,∠1、∠2、∠3、∠4、∠5在平面内围绕某一点拼接,所以∠1+∠2+∠3+∠4+∠5=360°。已知∠5=35°,则∠1+∠2+∠3+∠4=360°-35°=325°。
答案:C
答案:C
9. 图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始融化,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5= ______.
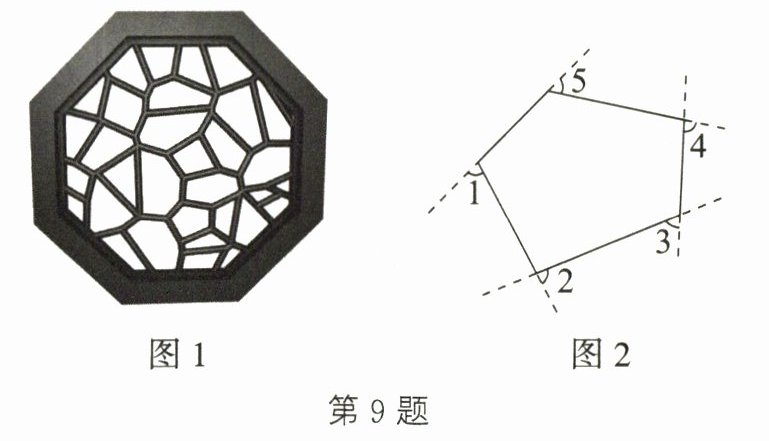

360°
答案:
解:由多边形外角和定理可知,任意多边形的外角和为360°。图中∠1、∠2、∠3、∠4、∠5是该五边形的五个外角,所以∠1+∠2+∠3+∠4+∠5=360°。
360°
360°
10. 六边形的内角和比它的外角和多
$360^\circ$
.
答案:
【解析】:
本题主要考查多边形的内角和与外角和的关系。
首先,需要知道多边形的内角和公式:对于一个n边形,其内角和为$(n-2) × 180^\circ$。
对于六边形,其内角和为:
$(6-2) × 180^\circ = 720^\circ$
其次,多边形的外角和总是固定的,为$360^\circ$。
因此,六边形的内角和比其外角和多出的度数为:
$720^\circ - 360^\circ = 360^\circ$
【答案】:
$360^\circ$
本题主要考查多边形的内角和与外角和的关系。
首先,需要知道多边形的内角和公式:对于一个n边形,其内角和为$(n-2) × 180^\circ$。
对于六边形,其内角和为:
$(6-2) × 180^\circ = 720^\circ$
其次,多边形的外角和总是固定的,为$360^\circ$。
因此,六边形的内角和比其外角和多出的度数为:
$720^\circ - 360^\circ = 360^\circ$
【答案】:
$360^\circ$
查看更多完整答案,请扫码查看


