《2025年多维互动提优课堂七年级数学上册苏科版》

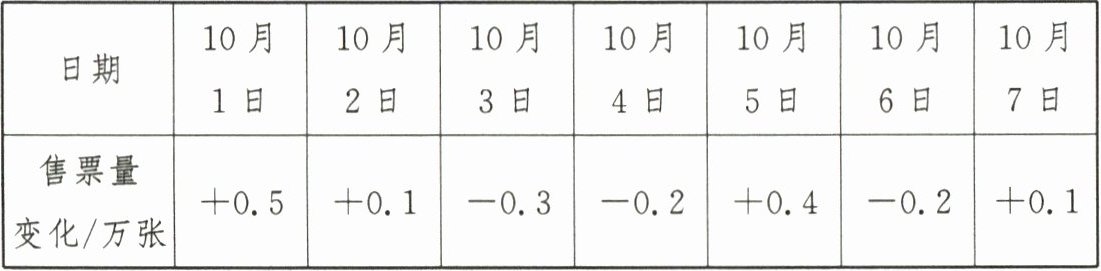
21. 某市2024年9月30日某电影的售票量为1.1万张,10月1日至10月7日售票量(单位：万张)变化如下表(“+”表示售票量比前一天多,“-”表示售票量比前一天少)：
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 售票量变化/万张 | +0.5 | +0.1 | -0.3 | -0.2 | +0.4 | -0.2 | +0.1 |

请根据以上信息,回答下列问题：
(1)10月2日的售票量为多少万张？
(2)10月7日与9月30日相比,哪一天的售票量多？
(3)若平均每张电影票的售价为45元,则10月1日到10月7日该市该电影的票房收入是多少万元？

答案：
(1)解：9月30日售票量为1.1万张，10月1日售票量为1.1 + 0.5 = 1.6万张，10月2日售票量为1.6 + 0.1 = 1.7万张。答：10月2日的售票量为1.7万张。
(2)解：10月3日售票量：1.7 - 0.3 = 1.4万张；10月4日售票量：1.4 - 0.2 = 1.2万张；10月5日售票量：1.2 + 0.4 = 1.6万张；10月6日售票量：1.6 - 0.2 = 1.4万张；10月7日售票量：1.4 + 0.1 = 1.5万张。因为1.5 ＞ 1.1，所以10月7日售票量多。答：10月7日售票量多。
(3)解：10月1日至7日售票量总和为1.6 + 1.7 + 1.4 + 1.2 + 1.6 + 1.4 + 1.5 = 10.4万张，票房收入为10.4×45 = 468万元。答：票房收入是468万元。

22. 规定一种新运算：a⊕b= ab+a+b+1.例如：3⊕4= 3×4+3+4+1= 20.
(1)① 计算：(-5)⊕3=-16,3⊕(-5)=-16.
② 试说明运算“⊕”具有交换律.
(2)① 计算：(-3)⊕(4⊕2)=-32,[(-3)⊕4]⊕2=-27.
② 由计算结果可得,运算“⊕”不具有(填“具有”或“不具有”)结合律.

答案： 【解析】：
本题主要考查了新定义运算以及交换律和结合律的判断。
(1)① 根据新定义的运算规则，我们可以将数值代入公式进行计算。
对于$(-5)⊕3$，我们有：
$(-5)⊕3 = (-5) × 3 + (-5) + 3 + 1 = -15 - 5 + 3 + 1 = -16$
对于$3⊕(-5)$，我们有：
$3⊕(-5) = 3 × (-5) + 3 + (-5) + 1 = -15 + 3 - 5 + 1 = -16$
② 要证明运算“⊕”具有交换律，我们需要证明$a⊕b = b⊕a$。
根据定义，我们有：
$a⊕b = ab + a + b + 1$
$b⊕a = ba + b + a + 1$
由于乘法的交换律，我们知道$ab = ba$，所以：
$a⊕b = ab + a + b + 1 = ba + b + a + 1 = b⊕a$
因此，运算“⊕”具有交换律。
(2)① 首先，我们需要计算内层的运算结果，然后再进行外层的运算。
对于$(-3)⊕(4⊕2)$，我们先计算$4⊕2$：
$4⊕2 = 4 × 2 + 4 + 2 + 1 = 8 + 4 + 2 + 1 = 15$
然后，我们计算$(-3)⊕15$：
$(-3)⊕15 = (-3) × 15 + (-3) + 15 + 1 = -45 - 3 + 15 + 1 = -32$
对于$[(-3)⊕4]⊕2$，我们先计算$(-3)⊕4$：
$(-3)⊕4 = (-3) × 4 + (-3) + 4 + 1 = -12 - 3 + 4 + 1 = -10$
然后，我们计算$(-10)⊕2$：
$(-10)⊕2 = (-10) × 2 + (-10) + 2 + 1 = -20 - 10 + 2 + 1 = -27$
② 通过比较两个表达式的计算结果，我们发现它们不相等（$-32 \neq -27$），所以运算“⊕”不具有结合律。
【答案】：
(1)① $-16$；$-16$
② 运算过程如上，结论是运算“⊕”具有交换律。
(2)① $-32$；$-27$
② 不具有