《2025年多维互动提优课堂七年级数学上册苏科版》

8. 已知$|a|= 6$,$b^2= 4$,且$a＜b$,则$\frac{1}{2}a - b$的值为(　　)A
A.$-5或-1$　　
B.$-5或5$　　
C.$-1或1$　　
D.$1或5$

答案： 解：
∵|a|=6，
∴a=±6.
∵b²=4，
∴b=±2.
∵a＜b，
当b=2时，a=-6（a=6不满足a＜2，舍去）；
当b=-2时，a=-6（a=6不满足a＜-2，舍去）.
情况1：a=-6，b=2时，
$\frac{1}{2}a - b=\frac{1}{2}×(-6)-2=-3-2=-5$.
情况2：a=-6，b=-2时，
$\frac{1}{2}a - b=\frac{1}{2}×(-6)-(-2)=-3+2=-1$.
综上，$\frac{1}{2}a - b$的值为-5或-1.
答案：A.

9. 如果收入50元记作+50元,那么支出30元记作-30元.

答案： 【解析】：
本题考查正负数在实际生活中的应用。题目中提到收入50元记作+50元，这里使用了正数来表示收入。根据正负数的相对意义，支出则应该用负数来表示。因此，支出30元应该记作-30元。
【答案】：
-30元

10. 单项式$-2x^2yz$的系数是$-2$,次数是$4$.

答案： 【解析】：
本题主要考查了单项式的系数和次数的定义。单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数。
对于单项式$-2x^2yz$，其数字因数是$-2$，所以系数是$-2$。
对于次数，需要计算所有字母的指数和。在$-2x^2yz$中，$x$的指数是$2$，$y$的指数是$1$，$z$的指数是$1$，所以次数是$2+1+1=4$。
【答案】：
系数是$-2$，次数是$4$。

11. 一个两位数,个位上的数字是$a$,十位上的数字是$b$,列式表示这个两位数：$10b + a$.

答案： 解：因为十位上的数字是$b$，表示$b$个十，即$10b$；个位上的数字是$a$，表示$a$个一，即$a$。所以这个两位数可以表示为$10b + a$。
$10b + a$

12. 比较大小：$-\pi$＜$-3.14$.(填“＞”“＜”或“=”)

答案： 【解析】：
本题考查实数的大小比较，特别是两个负数的大小比较。对于两个负数，绝对值大的数反而小。
首先计算两个数的绝对值，$|-π| = π$，$|-3.14| = 3.14$，已知$π$的近似值为$3.14159...$，比$3.14$大，所以，$|-π| ＞ |-3.14|$，根据负数的比较规则，得到$−π ＜ -3.14$。
【答案】：
＜

13. 数轴上与原点的距离小于$\frac{22}{7}$的整数点有7个.

答案： 【解析】：
本题主要考查数轴的概念以及绝对值的性质。
在数轴上，一个数与原点的距离等于该数的绝对值。
因此，题目要求找到与原点的距离小于$\frac{22}{7}$的整数点，即找到绝对值小于$\frac{22}{7}$的整数。
首先，确定$\frac{22}{7}$的整数部分，$\frac{22}{7} \approx 3.14$，
所以绝对值小于$\frac{22}{7}$的最大整数是3。
然后，考虑所有绝对值小于3的整数，它们分别是：-3，-2，-1，0，1，2，3。但由于3也满足条件（因为$3 ＜ \frac{22}{7}$），并且-3也满足（因为$|-3| = 3 ＜ \frac{22}{7}$），所以这些整数都符合条件。
最后，统计这些整数的个数，共有7个。
【答案】：
7

14. 若单项式$3x^{2m-2}y^n与-5x^my^3$是同类项,则$m+n= $5.

答案： 解：因为单项式$3x^{2m - 2}y^n$与$-5x^my^3$是同类项，所以相同字母的指数相同。
则有$2m - 2 = m$，解得$m = 2$；$n = 3$。
所以$m + n = 2 + 3 = 5$。
5

15. 若$x^p +4x^3 - qx^2 -2x +5是关于x$的五次四项式,则$-p + q= $-5.

答案： 解：因为$x^p +4x^3 - qx^2 -2x +5$是关于$x$的五次四项式，所以最高次项次数为$5$，即$p = 5$；又因为是四项式，所以合并同类项后只有四项，原多项式有五项，故其中一项系数为$0$，即$-q = 0$，$q = 0$。则$-p + q=-5 + 0=-5$。
$-5$

16. 若$|x|= 3$,$|y|= 7$,且$x - y＞0$,则$x + y= $-4或-10.

答案： 解：
∵|x|=3，|y|=7，
∴x=±3，y=±7。
∵x - y＞0，即x＞y，
∴当x=3时，y=-7；当x=-3时，y=-7。
当x=3，y=-7时，x + y=3 + (-7)=-4；
当x=-3，y=-7时，x + y=-3 + (-7)=-10。
综上，x + y=-4或-10。

17. 从$-1$,$-2$,$3$,$4$中取三个不同的数相乘,可得到的最大乘积是8,最小乘积是-24.

答案： 解：从-1，-2，3，4中取三个不同的数相乘，所有可能情况如下：
1. $(-1)×(-2)×3=6$
2. $(-1)×(-2)×4=8$
3. $(-1)×3×4=-12$
4. $(-2)×3×4=-24$
比较上述结果：最大乘积是8，最小乘积是-24。
8；-24

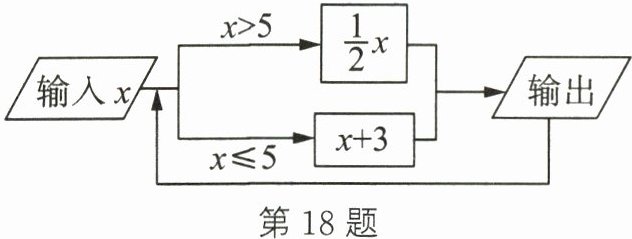
18. 按如图所示的程序运算,若输入的$x的值为-3$,则第100次输出的结果为______.

3

答案： 【解析】：本题可根据所给的程序运算规则，先求出前几次的输出结果，找出其规律，再根据规律求出第$100$次输出的结果。
步骤一：根据程序运算规则求出前几次的输出结果
已知输入的$x$的值为$-3$，因为$-3\leqslant5$，将$x = - 3$代入$x + 3$可得：$-3 + 3 = 0$，即第一次输出结果为$0$。
此时把$x = 0$再次输入程序，因为$0\leqslant5$，将$x = 0$代入$x + 3$可得：$0 + 3 = 3$，即第二次输出结果为$3$。
把$x = 3$输入程序，因为$3\leqslant5$，将$x = 3$代入$x + 3$可得：$3 + 3 = 6$，即第三次输出结果为$6$。
把$x = 6$输入程序，因为$6\gt5$，将$x = 6$代入$\frac{1}{2}x$可得：$\frac{1}{2}×6 = 3$，即第四次输出结果为$3$。
把$x = 3$输入程序，因为$3\leqslant5$，将$x = 3$代入$x + 3$可得：$3 + 3 = 6$，即第五次输出结果为$6$。
$\cdots$
步骤二：找出输出结果的规律
通过上述计算可以发现，从第二次开始，输出结果按照$3$，$6$循环出现。
步骤三：计算第$100$次输出的结果
因为第一次输出结果单独计算，从第二次开始循环，所以除去第一次，后面还有$100 - 1 = 99$次输出。
由于循环周期为$2$（即$3$，$6$为一个周期），用$99$除以$2$：$99÷2 = 49\cdots\cdots1$，其中$49$是商，表示完整的周期数，$1$是余数，表示循环$49$个周期后，下一个数就是第$100$次输出的结果。
一个周期中第一个数是$3$，所以第$100$次输出的结果为$3$。
【答案】：$3$

19. 计算：
(1)$(-3)-(-9)+7-8$；
(2)$\frac{1}{2}+\frac{5}{7}+(-\frac{1}{2})+\frac{2}{7}$；
(3)$(\frac{1}{9}+\frac{1}{6}-\frac{1}{3})÷(-\frac{1}{18})$；
(4)$(-2)^3×0.5^2+(-8)÷(-2)^2$.

答案：
(1)解：$(-3)-(-9)+7-8$
$=-3+9+7-8$
$=(-3-8)+(9+7)$
$=-11+16$
$=5$
(2)解：$\frac{1}{2}+\frac{5}{7}+(-\frac{1}{2})+\frac{2}{7}$
$=\left(\frac{1}{2}-\frac{1}{2}\right)+\left(\frac{5}{7}+\frac{2}{7}\right)$
$=0+1$
$=1$
(3)解：$(\frac{1}{9}+\frac{1}{6}-\frac{1}{3})÷(-\frac{1}{18})$
$=(\frac{1}{9}+\frac{1}{6}-\frac{1}{3})×(-18)$
$=\frac{1}{9}×(-18)+\frac{1}{6}×(-18)-\frac{1}{3}×(-18)$
$=-2-3+6$
$=1$
(4)解：$(-2)^3×0.5^2+(-8)÷(-2)^2$
$=-8×0.25+(-8)÷4$
$=-2-2$
$=-4$