《2025年多维互动提优课堂七年级数学上册苏科版》

20. 把下列各数填在相应的括号中.
$-5,10,0,2\frac{1}{3},-2.15,+66,-\frac{2}{5},15\%,-16,1.010010001…$(相邻两个 1 之间的 0 的个数逐次加 1),0.3,$\pi$.
正整数：{10, +66};
负整数：{-5, -16};
正有理数：{$10, 2\frac{1}{3}, +66, 15\%, 0.3$};
非负整数：{10, 0, +66}.

答案： 【解析】：
本题主要考查了有理数的分类，需要准确理解正整数、负整数、正有理数和非负整数的定义，然后根据这些定义将给定的数进行分类。
正整数：大于0的整数；
负整数：小于0的整数；
正有理数：大于0的有理数（包括正整数和正分数）；
非负整数：大于或等于0的整数。
根据以上定义，我们可以将给定的数进行分类：
正整数：从给定的数中找出大于0的整数，有$10, +66$；
负整数：从给定的数中找出小于0的整数，有$-5, -16$；
正有理数：从给定的数中找出大于0的有理数，包括正整数和正分数，有$10, 2\frac{1}{3}, +66, 15\%, 0.3$；
注意，虽然$1.010010001…$（相邻两个1之间的0的个数逐次加1）和$\pi$也是正数，但它们不是有理数，所以不归入此类；
非负整数：从给定的数中找出大于或等于0的整数，有$10, 0, +66$。
【答案】：
正整数：{$10, +66$}；
负整数：{$-5, -16$}；
正有理数：{$10, 2\frac{1}{3}, +66, 15\%, 0.3$}；
非负整数：{$10, 0, +66$}。

21. 幻方是一个古老的数学问题,我国古代的《洛书》中记载了最早的三阶幻方——九宫图. 如图所示的幻方中,每一横行、每一竖列以及每条对角线上的数字之和都等于 15,请补充完整.

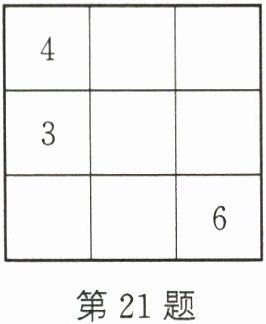
$\begin{array}{ccc}4 & 9 & 2 \\ 3 & 5 & 7 \\ 8 & 1 & 6\end{array}$

答案： 【解析】：
本题考查有理数的加减法。
幻方中，每一横行、每一竖列以及每条对角线上的数字之和都等于$15$。
设幻方中未知数字的位置如图所示：
$\begin{array}{ccc}4 & a & b \\ 3 & c & d \\ e & f & 6\end{array}$
根据幻方的性质，可以列出以下等式：
第一行：$4 + a + b = 15$，
第二行：$3 + c + d = 15$，
第三行：$e + f + 6 = 15$，
第一列：$4 + 3 + e = 15$，
第二列：$a + c + f = 15$，
第三列：$b + d + 6 = 15$，
主对角线：$4 + c + 6 = 15$，
副对角线：$b + c + e = 15$。
首先，解主对角线上的等式：
$4 + c + 6 = 15$，
$c = 5$。
然后，解第一列上的等式：
$4 + 3 + e = 15$，
$e = 8$。
接着，解第三行上的等式：
$e + f + 6 = 15$，
$8 + f + 6 = 15$，
$f = 1$。
再解第二列上的等式：
$a + c + f = 15$，
$a + 5 + 1 = 15$，
$a = 9$。
接着，解第一行上的等式：
$4 + a + b = 15$，
$4 + 9 + b = 15$，
$b = 2$。
最后，解第二行和第三列上的等式：
$3 + c + d = 15$，
$3 + 5 + d = 15$，
$d = 7$。
$b + d + 6 = 15$，
$2 + 7 + 6 = 15$（验证无误）。
因此，幻方补充完整后为：
$\begin{array}{ccc}4 & 9 & 2 \\ 3 & 5 & 7 \\ 8 & 1 & 6\end{array}$
【答案】：
$\begin{array}{ccc}4 & 9 & 2 \\ 3 & 5 & 7 \\ 8 & 1 & 6\end{array}$

22. 定义新运算: $m*n= (m-n)^n+n-m$,如 $3*2= (3-2)^2+2-3= 1^2+2-3= 0$.
(1) 求 $(-1)*3$ 的值.
(2) 若 $b= 2$,且 $a*b+a+|c+5|= 2$,求 $c*a$ 的值.

答案： 【解析】：
本题主要考查了新定义运算及代数式的代入计算。
(1) 根据新定义的运算规则，我们可以将$(-1)*3$转化为标准的数学运算。
(2) 已知$b=2$，我们需要先根据新定义的运算求出$a*b$，然后将其与$a$和$|c+5|$相加，根据和为2的条件来求解$a$和$c$的值，最后根据新定义的运算求出$c*a$。
【答案】：
(1)
解：根据新定义的运算规则，我们有
$(-1)*3 = (-1-3)^3 + 3 - (-1)$
$= (-4)^3 + 3 + 1$
$= -64 + 4$
$= -60$
(2)
当$b=2$时，
$a*b = (a-2)^2 + 2 - a$
$= a^2 - 4a + 4 + 2 - a$
$= a^2 - 5a + 6$
所以，
$a*b + a + |c+5| = a^2 - 5a + 6 + a + |c+5|$
$= a^2 - 4a + 6 + |c+5|$
由题意知，
$a^2 - 4a + 6 + |c+5| = 2$
移项得，
$a^2 - 4a + 4 + |c+5| = 0$
即，
$(a-2)^2 + |c+5| = 0$
由于平方和绝对值都是非负的，所以要使上式成立，必须有，
$(a-2)^2 = 0$ 和 $|c+5| = 0$
解得，
$a = 2$，$c = -5$
所以，
$c*a = (-5)*2$
$= (-5-2)^2 + 2 - (-5)$
$= 49 + 2 + 5$
$= 56$