第87页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
12. (2024·晋中榆次区期末)如图,$\angle AOB$与 $\angle COD$都是直角。
(1)若 $\angle BOC = 113^{\circ}$,试求 $\angle AOD$的度数。
(2)以 OD 为一边,作 $\angle DOE = \angle DOB$,且 OE 与 OB 不重合。(要求:尺规作图,保留作图痕迹)
(3)在(2)的条件下,如果 $\angle AOD$的度数比 $\angle BOD$度数的 3 倍还多 $10^{\circ}$,那么 $\angle AOE$的度数为

(1)若 $\angle BOC = 113^{\circ}$,试求 $\angle AOD$的度数。
(2)以 OD 为一边,作 $\angle DOE = \angle DOB$,且 OE 与 OB 不重合。(要求:尺规作图,保留作图痕迹)
(3)在(2)的条件下,如果 $\angle AOD$的度数比 $\angle BOD$度数的 3 倍还多 $10^{\circ}$,那么 $\angle AOE$的度数为
50°
。
答案:
12.
(1)
∵ ∠AOB与∠COD都是直角,
∴ ∠AOB = ∠COD = 90°.
∵ ∠BOC = 113°.
∴ ∠BOD = ∠BOC - ∠COD = 113° - 90° = 23°.
∴ ∠AOD = ∠AOB - ∠BOD = 90° - 23° = 67°.
(2)图略.
(3)50°
(1)
∵ ∠AOB与∠COD都是直角,
∴ ∠AOB = ∠COD = 90°.
∵ ∠BOC = 113°.
∴ ∠BOD = ∠BOC - ∠COD = 113° - 90° = 23°.
∴ ∠AOD = ∠AOB - ∠BOD = 90° - 23° = 67°.
(2)图略.
(3)50°
13. (2024·太原第二外国语月考)从 n 边形的一个顶点出发作对角线,可以把这个 n 边形分成 9 个三角形,则 n =(
A.9
B.10
C.11
D.12
C
)A.9
B.10
C.11
D.12
答案:
13.C
14. (2024·太原晋源区月考)一个扇形的圆心角为 $120^{\circ}$,半径为 3,则这个扇形的面积为
3π
(结果保留 $\pi$)。
答案:
14.3π
15. (2024·运城河津市期末)阅读与思考
数学课快结束时,老师总结:“尺规作图指利用无刻度的直尺和圆规作图,其中圆规的作用为截取等长,它可以精确地截取或构造出与已知线段等长的线段。同学们,大家可以思考如何利用尺规作图直观比较线段的长度,比较角的度数,也可以思考利用尺规作图还可以解决哪些生活中的问题呢?”课后数学社团的同学们积极思考,内容如下:
小颖的思考:如何利用尺规作图比较线段的长短,给出具体做法。
例如:如图 1,线段 AB 上有两个定点 M,N,利用尺规作图可以直观比较 AM + BN 与 MN 之间的长度关系,作图过程如下:

如图 2,以点 M 为圆心,AM 的长为半径画弧,交 AB 于点 $A'$,再以点 $A'$为圆心,BN 的长为半径画弧,交 AB 于点 $B'$,因为 $MA' + A'B' > MN$,所以 AM + BN > MN。

小鹏的思考:如何利用尺规作图比较角的度数并提出问题。
问题 1:如图 3,在 $\angle AOB$的内部有两条射线 OM,ON,如何利用尺规作图直观比较 $\angle AOM + \angle BON$与 $\angle MON$之间的大小关系?
小丽的思考:如何利用尺规作图解决一些生活中的问题,她想到下面的生活经历并提出问题。
图 4 为棒球场地,已知本垒到一垒,一垒到二垒,二垒到三垒,三垒到本垒的距离均相等,但一场暴雨冲刷过后,二垒和三垒的位置被泥土覆盖了,图 5 为其抽象出的示意图。
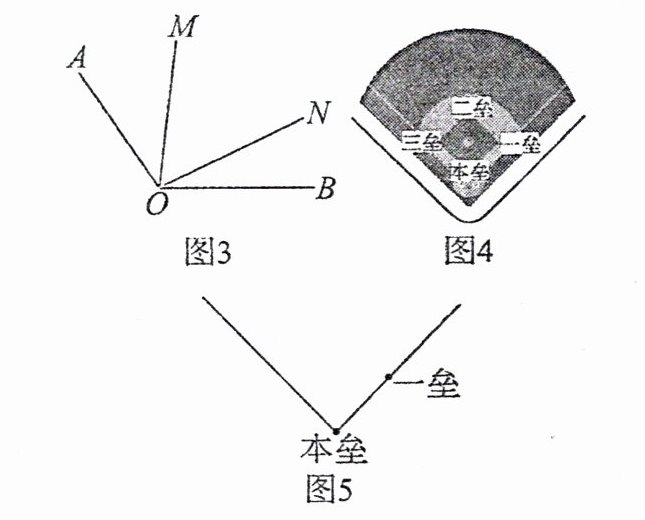
问题 2:利用圆规在图 5 中找出二垒和三垒的准确位置。
任务:
(1)请你解决小鹏思考中提出的问题 1 并完成填空。
①利用尺规在图 3 中画出直观比较 $\angle AOM + \angle BON$与 $\angle MON$之间的大小关系的过程(请保留作图痕迹)。
②填空:问题 1 中的结论为 $\angle AOM + \angle BON$
(2)请你解决小丽思考中提出的问题 2:利用圆规在图 5 中画出二垒和三垒的准确位置(请保留作图痕迹)。
数学课快结束时,老师总结:“尺规作图指利用无刻度的直尺和圆规作图,其中圆规的作用为截取等长,它可以精确地截取或构造出与已知线段等长的线段。同学们,大家可以思考如何利用尺规作图直观比较线段的长度,比较角的度数,也可以思考利用尺规作图还可以解决哪些生活中的问题呢?”课后数学社团的同学们积极思考,内容如下:
小颖的思考:如何利用尺规作图比较线段的长短,给出具体做法。
例如:如图 1,线段 AB 上有两个定点 M,N,利用尺规作图可以直观比较 AM + BN 与 MN 之间的长度关系,作图过程如下:

如图 2,以点 M 为圆心,AM 的长为半径画弧,交 AB 于点 $A'$,再以点 $A'$为圆心,BN 的长为半径画弧,交 AB 于点 $B'$,因为 $MA' + A'B' > MN$,所以 AM + BN > MN。

小鹏的思考:如何利用尺规作图比较角的度数并提出问题。
问题 1:如图 3,在 $\angle AOB$的内部有两条射线 OM,ON,如何利用尺规作图直观比较 $\angle AOM + \angle BON$与 $\angle MON$之间的大小关系?
小丽的思考:如何利用尺规作图解决一些生活中的问题,她想到下面的生活经历并提出问题。
图 4 为棒球场地,已知本垒到一垒,一垒到二垒,二垒到三垒,三垒到本垒的距离均相等,但一场暴雨冲刷过后,二垒和三垒的位置被泥土覆盖了,图 5 为其抽象出的示意图。

问题 2:利用圆规在图 5 中找出二垒和三垒的准确位置。
任务:
(1)请你解决小鹏思考中提出的问题 1 并完成填空。
①利用尺规在图 3 中画出直观比较 $\angle AOM + \angle BON$与 $\angle MON$之间的大小关系的过程(请保留作图痕迹)。
②填空:问题 1 中的结论为 $\angle AOM + \angle BON$
>
$\angle MON$。(“>”“<”或“=”)(2)请你解决小丽思考中提出的问题 2:利用圆规在图 5 中画出二垒和三垒的准确位置(请保留作图痕迹)。
答案:
15.
(1)①图3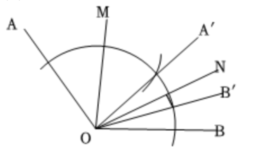 ,以点O为圆心,适当长为半径画弧,分别交OA,OM,ON,OB于点C,D,H,G,以点D为圆心,CD的长为半径画弧,交弧CG于点E,以点E为圆心,GH的长为半径画弧,交弧CG于点F,连接OE并延长得到边OA',连接OF并延长得到边OB'. ② >
,以点O为圆心,适当长为半径画弧,分别交OA,OM,ON,OB于点C,D,H,G,以点D为圆心,CD的长为半径画弧,交弧CG于点E,以点E为圆心,GH的长为半径画弧,交弧CG于点F,连接OE并延长得到边OA',连接OF并延长得到边OB'. ② >
(2)图5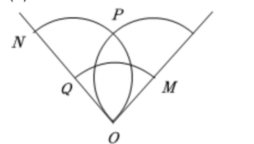 ,点P(二垒),Q(三垒)即为所求.
,点P(二垒),Q(三垒)即为所求.
15.
(1)①图3
 ,以点O为圆心,适当长为半径画弧,分别交OA,OM,ON,OB于点C,D,H,G,以点D为圆心,CD的长为半径画弧,交弧CG于点E,以点E为圆心,GH的长为半径画弧,交弧CG于点F,连接OE并延长得到边OA',连接OF并延长得到边OB'. ② >
,以点O为圆心,适当长为半径画弧,分别交OA,OM,ON,OB于点C,D,H,G,以点D为圆心,CD的长为半径画弧,交弧CG于点E,以点E为圆心,GH的长为半径画弧,交弧CG于点F,连接OE并延长得到边OA',连接OF并延长得到边OB'. ② > (2)图5
 ,点P(二垒),Q(三垒)即为所求.
,点P(二垒),Q(三垒)即为所求. 查看更多完整答案,请扫码查看


