第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
5. 如图,$ C $ 为线段 $ AB $ 上的一点,$ D $ 为 $ BC $ 的中点,点 $ C $ 把线段 $ AD $ 分成两部分,其中 $ AC:CD = 4:1 $,且 $ AB = 12 $。
(1)求 $ AC $ 的长。
(2)若点 $ E $ 在线段 $ AB $ 所在的直线上,且 $ AE = 3 $,求 $ DE $ 的长。

(1)求 $ AC $ 的长。
(2)若点 $ E $ 在线段 $ AB $ 所在的直线上,且 $ AE = 3 $,求 $ DE $ 的长。

答案:
5. 解:
(1)
∵D为BC的中点,
∴BC=2CD=2BD.
∵AC:CD=4:1,
∴AC=4CD.
∴AB=AC + BC=4CD + 2CD=12,解得CD=2.
∴AC=4CD=4×2=8.
(2)①如图1,当点E在线段AB上时,
DE=AB - AE - DB=12 - 3 - 2=7;
②如图2,当点E在线段BA的延长线上,
DE=AB + AE - BD=12 + 3 - 2=13.
综上所述,DE的长为7或13.
(1)
∵D为BC的中点,
∴BC=2CD=2BD.
∵AC:CD=4:1,
∴AC=4CD.
∴AB=AC + BC=4CD + 2CD=12,解得CD=2.
∴AC=4CD=4×2=8.
(2)①如图1,当点E在线段AB上时,
DE=AB - AE - DB=12 - 3 - 2=7;
②如图2,当点E在线段BA的延长线上,
DE=AB + AE - BD=12 + 3 - 2=13.
综上所述,DE的长为7或13.
6. (2024·大同新荣区期末联考)阅读材料:数学课上,老师给出了如下问题:如图 1,$ \angle AOB = 80^{\circ} $,$ OC $ 平分 $ \angle AOB $. 若 $ \angle BOD = 20^{\circ} $,请补全图形,并求 $ \angle COD $ 的度数。
以下是小明的解答过程:
解:如图 2,$ \because OC $ 平分 $ \angle AOB $,$ \angle AOB = 80^{\circ} $,$ \therefore \angle BOC = $
小静说:“我觉得这道题有两种情况,小明考虑的是 $ OD $ 在 $ \angle AOB $ 外部的情况,事实上,$ OD $ 还可能在 $ \angle AOB $ 的内部。”
请解答下列问题:
(1)请将小明的解答过程补充完整。
(2)根据小静的想法,请在图 3 中画出另一种情况对应的图形,并求出此时 $ \angle COD $ 的度数。
(3)小静的思考方法所体现出来的数学思想是
A. 分类讨论思想
B. 整体思想
C. 数形结合思想

以下是小明的解答过程:
解:如图 2,$ \because OC $ 平分 $ \angle AOB $,$ \angle AOB = 80^{\circ} $,$ \therefore \angle BOC = $
$\frac{1}{2}$
$ \angle AOB = $40°
. $ \because \angle BOD = 20^{\circ} $,$ \therefore \angle COD = \angle BOD + \angle BOC = $60°
.小静说:“我觉得这道题有两种情况,小明考虑的是 $ OD $ 在 $ \angle AOB $ 外部的情况,事实上,$ OD $ 还可能在 $ \angle AOB $ 的内部。”
请解答下列问题:
(1)请将小明的解答过程补充完整。
(2)根据小静的想法,请在图 3 中画出另一种情况对应的图形,并求出此时 $ \angle COD $ 的度数。
(3)小静的思考方法所体现出来的数学思想是
A
(填字母序号)。A. 分类讨论思想
B. 整体思想
C. 数形结合思想

答案:
6. 解:
(1)$\frac{1}{2}$ 40° 60°
(2)图3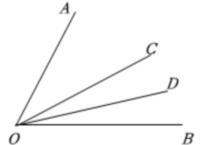
∵OC平分∠AOB,∠AOB=80°,
∴∠BOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×80°=40°.
∵∠BOD=20°,
∴∠COD=∠BOC - ∠BOD=40° - 20°=20°.
(3)A
6. 解:
(1)$\frac{1}{2}$ 40° 60°
(2)图3

∵OC平分∠AOB,∠AOB=80°,
∴∠BOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×80°=40°.
∵∠BOD=20°,
∴∠COD=∠BOC - ∠BOD=40° - 20°=20°.
(3)A
7. 将长方形纸片 $ ABCD $ 按如图所示方式折叠,使得 $ \angle A' EB' = 40^{\circ} $,其中 $ EF $,$ EG $ 为折痕,则 $ \angle FEG $ 的度数为(

A.$ 40^{\circ} $
B.$ 70^{\circ} $
C.$ 100^{\circ} $
D.$ 110^{\circ} $
D
)
A.$ 40^{\circ} $
B.$ 70^{\circ} $
C.$ 100^{\circ} $
D.$ 110^{\circ} $
答案:
7. D
8. (2024·晋中榆社县期末)综合与探究
【初步探究】
(1)如图 1,已知线段 $ AB = 16 $,$ C $,$ D $ 为线段 $ AB $ 上的两个动点,且 $ CD = 4 $,$ M $,$ N $ 分别是 $ AC $ 和 $ BD $ 的中点,求线段 $ MN $ 的长。
【类比探究】
(2)如图 2,直角 $ \angle COD $ 与平角 $ \angle AOB $ 摆放在一起,且 $ OM $ 和 $ ON $ 分别是 $ \angle AOC $,$ \angle BOD $ 的平分线,求 $ \angle MON $ 的度数。
【知识迁移】
(3)当 $ \angle AOB = \alpha $,$ \angle COD = \beta (0^{\circ} \lt \alpha \lt 180^{\circ} $,$ 0^{\circ} \lt \beta \lt 180^{\circ}) $ 时,如图 3 摆放在一起,且 $ OM $ 和 $ ON $ 分别是 $ \angle AOC $,$ \angle BOD $ 的平分线,求 $ \angle MON $ 的度数(用含 $ \alpha $,$ \beta $ 的代数式表示)。


【初步探究】
(1)如图 1,已知线段 $ AB = 16 $,$ C $,$ D $ 为线段 $ AB $ 上的两个动点,且 $ CD = 4 $,$ M $,$ N $ 分别是 $ AC $ 和 $ BD $ 的中点,求线段 $ MN $ 的长。
【类比探究】
(2)如图 2,直角 $ \angle COD $ 与平角 $ \angle AOB $ 摆放在一起,且 $ OM $ 和 $ ON $ 分别是 $ \angle AOC $,$ \angle BOD $ 的平分线,求 $ \angle MON $ 的度数。
【知识迁移】
(3)当 $ \angle AOB = \alpha $,$ \angle COD = \beta (0^{\circ} \lt \alpha \lt 180^{\circ} $,$ 0^{\circ} \lt \beta \lt 180^{\circ}) $ 时,如图 3 摆放在一起,且 $ OM $ 和 $ ON $ 分别是 $ \angle AOC $,$ \angle BOD $ 的平分线,求 $ \angle MON $ 的度数(用含 $ \alpha $,$ \beta $ 的代数式表示)。


答案:
8. 解:
(1)因为AB=16,CD=4,所以AC + BD=AB - CD=16 - 4=12.因为M,N分别是AC和BD的中点,所以MC=$\frac{1}{2}$AC,DN=$\frac{1}{2}$BD.所以MC + DN=$\frac{1}{2}$(AC + BD)=$\frac{1}{2}$×12=6.所以MN=MC + CD + DN =6 + 4=10.
(2)因为∠AOB=180°,∠COD=90°,所以∠AOC + ∠BOD=∠AOB - ∠COD=180° - 90°=90°.因为OM和ON分别是∠AOC,∠BOD的平分线,所以∠MOC=$\frac{1}{2}$∠AOC,∠DON=$\frac{1}{2}$∠BOD.所以∠MOC + ∠DON=$\frac{1}{2}$(∠AOC + ∠BOD)=$\frac{1}{2}$×90°=45°.所以∠MON=∠MOC + ∠COD + ∠DON=90° + 45°=135°.
(3)因为OM和ON分别是∠AOC,∠BOD的平分线,所以∠MOC=$\frac{1}{2}$∠AOC,∠BON=$\frac{1}{2}$∠BOD.所以∠MON=∠MOC + ∠COB + ∠BON=$\frac{1}{2}$∠AOC + ∠COB +$\frac{1}{2}$∠BOD=$\frac{1}{2}$(∠AOC + 2∠COB + ∠BOD)=$\frac{1}{2}$(∠AOB + ∠COD)=$\frac{1}{2}$(α + β).
(1)因为AB=16,CD=4,所以AC + BD=AB - CD=16 - 4=12.因为M,N分别是AC和BD的中点,所以MC=$\frac{1}{2}$AC,DN=$\frac{1}{2}$BD.所以MC + DN=$\frac{1}{2}$(AC + BD)=$\frac{1}{2}$×12=6.所以MN=MC + CD + DN =6 + 4=10.
(2)因为∠AOB=180°,∠COD=90°,所以∠AOC + ∠BOD=∠AOB - ∠COD=180° - 90°=90°.因为OM和ON分别是∠AOC,∠BOD的平分线,所以∠MOC=$\frac{1}{2}$∠AOC,∠DON=$\frac{1}{2}$∠BOD.所以∠MOC + ∠DON=$\frac{1}{2}$(∠AOC + ∠BOD)=$\frac{1}{2}$×90°=45°.所以∠MON=∠MOC + ∠COD + ∠DON=90° + 45°=135°.
(3)因为OM和ON分别是∠AOC,∠BOD的平分线,所以∠MOC=$\frac{1}{2}$∠AOC,∠BON=$\frac{1}{2}$∠BOD.所以∠MON=∠MOC + ∠COB + ∠BON=$\frac{1}{2}$∠AOC + ∠COB +$\frac{1}{2}$∠BOD=$\frac{1}{2}$(∠AOC + 2∠COB + ∠BOD)=$\frac{1}{2}$(∠AOB + ∠COD)=$\frac{1}{2}$(α + β).
查看更多完整答案,请扫码查看


