《2025年启东中学作业本九年级数学上册苏科版连淮专版》

1. 以平面直角坐标系的原点O为圆心,$\sqrt{2}为半径作\odot O$,则点$P(-1,1)与\odot O$的位置关系是(B)
A.在$\odot O$内
B.在$\odot O$上
C.在$\odot O$外
D.不能确定

答案： B

2. (2024·吉林)如图,四边形ABCD内接于$\odot O$,过点B作$BE// AD$,交CD于点E.若$∠BEC= 50^{\circ}$,则$∠ABC$的度数是(C)
A.$50^{\circ}$
B.$100^{\circ}$
C.$130^{\circ}$
D.$150^{\circ}$

答案： C

3. 如图,在$\triangle ABC$中,$CA= CB= 4$,$∠BAC= \alpha$,将$\triangle ABC$绕点A逆时针旋转$2\alpha$,得到$\triangle AB'C'$,连接$B'C$并延长交AB于点D,当$B'D\perp AB$时,$\overparen{BB'}$的长是(B)
A.$\frac{2\sqrt{3}}{3}\pi$
B.$\frac{4\sqrt{3}}{3}\pi$
C.$\frac{8\sqrt{3}}{9}\pi$
D.$\frac{10\sqrt{3}}{9}\pi$

答案： B

4. (2024·南京模拟)如图,在$Rt\triangle ABC$中,$∠ABC= 90^{\circ}$,BD为$\odot O$的切线,D为切点,若$DA= DE$,则$\frac{S_{\triangle ABD}}{S_{\triangle CDE}}= $B
A.$\frac{1}{3}$
B.$\frac{1}{2}$
C.$\frac{\sqrt{2}}{2}$
D.$\sqrt{2}-1$

答案： B

5. (2024·齐齐哈尔)若圆锥的底面半径是1cm,它的侧面展开图的圆心角是直角,则该圆锥的高为$\sqrt{15}$cm.

答案： $\sqrt{15}$

6. (2024·牡丹江)如图,在$\odot O$中,直径$AB\perp CD$于点E,$CD= 6$,$BE= 1$,则弦AC的长为$3\sqrt{10}$.

答案： $3\sqrt{10}$

7. (2024·秦淮区模拟)已知AB,CD分别是$\odot O$的内接正十边形和正五边形的边,AD,BC交于点P,则$∠APC$的度数为$126^{\circ}$.

答案： $126^{\circ}$

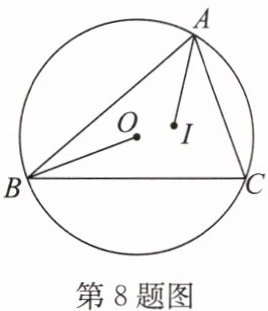
8. (2024·玄武区模拟)如图,点O是$\triangle ABC$外接圆的圆心,点I是$\triangle ABC$的内心,连接OB,IA.若$∠CAI= 35^{\circ}$,则$∠OBC$的度数为______$20^{\circ}$.

答案： $20^{\circ}$

9. (2024·高邮一模)如图,在$\triangle ABC$中,$∠A= 72^{\circ}$,$BC= 10$,若以BC为直径作$\odot O$分别交AB,AC于点M,N,则图中阴影部分的面积为______.(结果保留π)

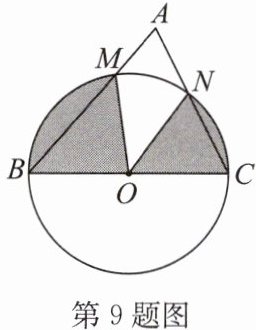
$10\pi$

答案： $10\pi$