《2025年启东中学作业本九年级数学上册苏科版连淮专版》

1.(2024·广东)综合与实践
【主题】滤纸与漏斗
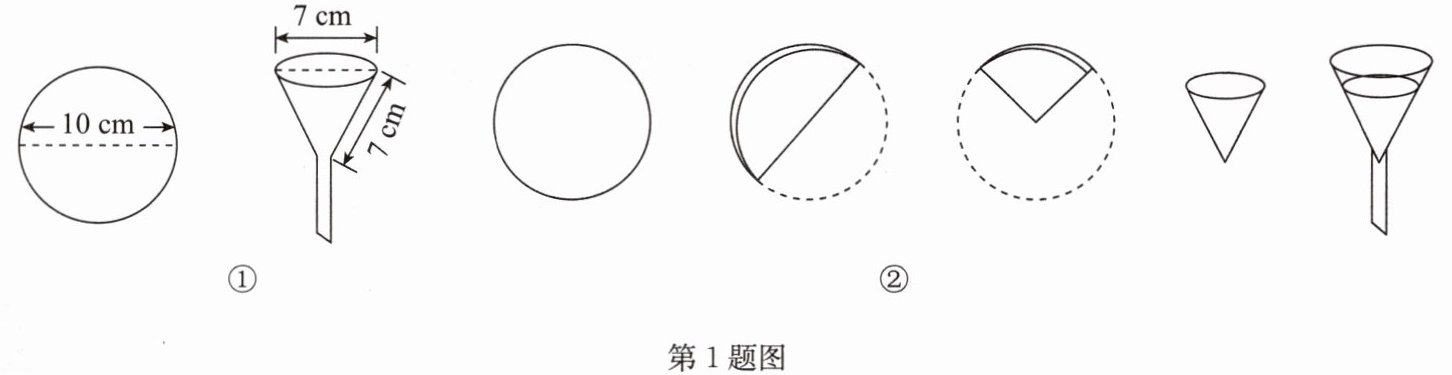
【素材】如图①所示.
①一张直径为10 cm的圆形滤纸；
②一只漏斗口直径与母线均为7 cm的圆锥形过滤漏斗.
【实践操作】如图②.
步骤1:取一张滤纸；
步骤2:按图示步骤折叠好滤纸；
步骤3:将其中一层撑开,围成圆锥形；
步骤4:将围成圆锥形的滤纸放入如图①所示漏斗中.
【实践探索】
(1)滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处)? 用你所学的数学知识说明.
(2)当滤纸紧贴漏斗内壁时,求滤纸围成圆锥形的体积.(结果保留π)

答案：
1.解:
(1)滤纸能紧贴此漏斗内壁，理由如下:
　由题意，得围成圆锥形滤纸的扇形圆心角$n_1$的度数为$180^{\circ}$。
　设圆锥形漏斗所对应的扇形圆心角的度数为$n_2^{\circ}$。
　根据题意，得$7\pi=\frac{n_2\pi×7}{180}$，解得$n_2 = 180$，$\therefore n_1=n_2$，
　$\therefore$滤纸能紧贴此漏斗内壁。
(2)如答图，过点$C$作$CF⊥DE$于点$F$，由
(1)知$CD = CE = 5cm$。
　由题意，得圆锥形滤纸的底面周长为$\frac{1}{2}×10\pi = 5\pi(cm)$，$\therefore DE\cdot\pi = 5\pi cm$，$\therefore DE = 5cm$。
　$\because CF⊥DE$，$CD = CE$，
　$\therefore DF=\frac{1}{2}DE=\frac{5}{2}cm$。
　在$Rt△CDF$中，$CF=\sqrt{CD^{2}-DF^{2}}=\frac{5\sqrt{3}}{2}cm$。
　$\therefore V=\pi\cdot(\frac{5}{2})^{2}×\frac{5\sqrt{3}}{2}×\frac{1}{3}=\frac{125\sqrt{3}}{24}\pi(cm^{3})$。
　即滤纸围成圆锥形的体积是$\frac{125\sqrt{3}}{24}\pi cm^{3}$。