《2025年启东中学作业本九年级数学上册苏科版连淮专版》

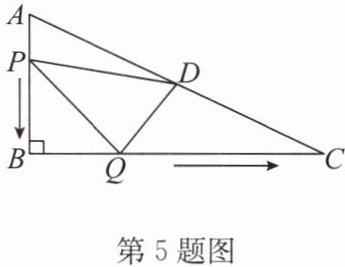
5. 如图,在△ABC中,∠B= 90°,AB= 12 cm,BC= 24 cm,动点P从点A出发沿边AB向点B以2 cm/s的速度移动,同时动点Q从点B出发沿边BC向点C以4 cm/s的速度移动,当点P运动到点B时,P,Q两点同时停止运动,设运动时间为t s.
(1)BP=(12 - 2t)cm,BQ=4tcm；(用含t的代数式表示)
(2)D是AC的中点,连接PD,QD,PQ.当t为何值时,△PDQ的面积为$40 cm^2？$

解:如答图，过点D作DH⊥BC于点H.∵∠B = 90°,即AB⊥BC,∴AB//DH;又∵D是AC的中点,∴BH = $\frac{1}{2}$BC = 12 cm,DH是△ABC的中位线,∴DH = $\frac{1}{2}$AB = 6 cm.根据题意，得$\frac{1}{2}$×12×24 - $\frac{1}{2}$×4t×(12 - 2t) - $\frac{1}{2}$×(24 - 4t)×6 - $\frac{1}{2}$×2t×12 = 40,整理,得t² - 6t + 8 = 0,解得t₁ = 2,t₂ = 4,即当t的值为2或4时,△PDQ的面积是40 cm².

答案：
(1) (12 - 2t)　4t
(2) 解:如答图，过点D作DH⊥BC于点H.
∵∠B = 90°,即AB⊥BC,
∴AB//DH;又
∵D是AC的中点,
∴BH = $\frac{1}{2}$BC = 12 cm,DH是△ABC的中位线,
∴DH = $\frac{1}{2}$AB = 6 cm.根据题意，得$\frac{1}{2}$×12×24 - $\frac{1}{2}$×4t×(12 - 2t) - $\frac{1}{2}$×(24 - 4t)×6 - $\frac{1}{2}$×2t×12 = 40,整理,得t² - 6t + 8 = 0,解得t₁ = 2,t₂ = 4,即当t的值为2或4时,△PDQ的面积是40 cm².

6. 如图,射线AC与射线CB垂直,C为垂足,且AC= 6 cm,点P从点A开始沿射线AC方向以2 cm/s的速度移动,点Q从点C开始沿射线CB方向以1 cm/s的速度移动.如果点P,Q分别从点A,C同时出发,运动的时间为t s.在运动的过程中,是否存在某一时刻,使得△PQC的面积是$4 cm^2？$若存在,求出t的值；若不存在,说明理由.

答案： 解:存在.由题意，得AP = 2t cm,CQ = t cm,① 当0 ＜ t ＜ 3时,PC = (6 - 2t)cm,
∴S△PCQ = $\frac{1}{2}$PC·QC = $\frac{1}{2}$t(6 - 2t),
∴$\frac{1}{2}$t(6 - 2t) = 4,即t² - 3t + 4 = 0.
∵b² - 4ac = -7 ＜ 0,
∴该方程无实数根,
∴该范围内不存在;② 当t ＞ 3时,PC = (2t - 6)cm,
∴S△PCQ = $\frac{1}{2}$PC·QC = $\frac{1}{2}$t(2t - 6),
∴$\frac{1}{2}$t(2t - 6) = 4,即t² - 3t - 4 = 0,解得t = 4或t = -1(舍去).综上所述，当t = 4时,△PQC的面积是4 cm².

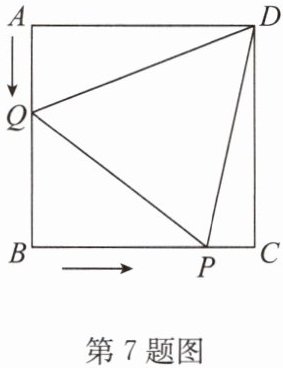
7. (2024·连云区月考)如图,正方形ABCD的边长为4 cm,动点P从点B出发,以2 cm/s的速度沿B→C→D方向,向点D运动；动点Q从点A出发,以1 cm/s的速度沿A→B方向,向点B运动.若P,Q两点同时出发,运动时间为t s.
(1)连接PD,PQ,DQ,当t为何值时,△PQD的面积为$11 cm^2？$
(2)当点P在BC上运动时,是否存在某一时刻,使得△PQD是以PD为腰的等腰三角形？若存在,请求出符合条件的t的值；若不存在,请说明理由.

答案：
(1) 当点P在BC上时,0 ≤ t ≤ 2,AQ = t cm,BQ = (4 - t)cm,BP = 2t cm,PC = (4 - 2t)cm,
∵S△PDQ = S正方形ABCD - S△ADQ - S△BPQ - S△CPD,
∴16 - $\frac{1}{2}$×4t - $\frac{1}{2}$(4 - t)·2t - $\frac{1}{2}$×4×(4 - 2t) = 11,整理,得t² - 2t - 3 = 0,解得t₁ = -1,t₂ = 3,均不合题意,舍去;当点P在CD上时,2 ＜ t ≤ 4,AQ = t cm,DP = (8 - 2t)cm,
∵S△PDQ = $\frac{1}{2}$BC·DP,
∴$\frac{1}{2}$×4(8 - 2t) = 11,解得t = $\frac{5}{4}$(不合题意，舍去).
∴不存在t的值，使△PQD的面积为11 cm².
(2) 存在.由题意,得AQ = t cm,BQ = (4 - t)cm,BP = 2t cm,PC = (4 - 2t)cm,0 ≤ t ≤ 2.当DP = DQ时,
∵DC = DA,
∴Rt△DPC≌Rt△DQA,
∴PC = AQ,即4 - 2t = t,解得t = $\frac{4}{3}$;当PD = PQ时,在Rt△PBQ中,PQ² = PB² + BQ² = (2t)² + (4 - t)²,在Rt△PCD中,PD² = PC² + CD² = (4 - 2t)² + 4²,
∴(2t)² + (4 - t)² = (4 - 2t)² + 4²,整理,得t² + 8t - 16 = 0,解得t₁ = -4$\sqrt{2}$ - 4(舍去),t₂ = 4$\sqrt{2}$ - 4.综上，当t的值为$\frac{4}{3}$或4$\sqrt{2}$ - 4时,△PDQ是以PD为腰的等腰三角形.