第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1. 一个人患了流感,经过两轮传染后共有64人患了流感. 设每轮传染中平均一个人传染的人数相等,求经过三轮传染后患流感的人数.
答案:
解:设每轮传染中平均一个人传染的人数为x,根据题意,得1+x+x(1+x)=64,解得x1=7,x2=−9(舍去),
∴64(1+x)=64×(1+7)=512.答:经过三轮传染后患流感的人数为512.
∴64(1+x)=64×(1+7)=512.答:经过三轮传染后患流感的人数为512.
2. (2024·雨花台区期末)某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出
9
个小分支.
答案:
9
3. 一个小组有若干人,新年互送贺卡,若全组共送贺卡72张,则这个小组有多少人?
答案:
解:设这个小组有x人,根据题意,得x(x−1)=72,解得x1=9,x2=−8(舍去).答:这个小组有9人.
4. 新情境 (2024·邗江区三模)为增强学生身体素质,提高学生篮球运动竞技水平,某市开展“市长杯”篮球比赛,赛制为单循环形式(每两队之间赛一场). 现计划赛程3天,每天安排5场比赛,则应邀请多少支球队参赛?
答案:
解:设应邀请x支球队参赛,根据题意,得$\frac{1}{2}$x(x−1)=5×3,解得x1=6,x2=−5(不符合题意,舍去).答:应邀请6支球队参赛.
5. (2024·南通期末)某商场以每件20元的价格购进一种商品,经市场调查发现:该商品每天的销售量y(件)与每件售价x(元)之间满足一次函数关系,其图像如图所示. 设该商场销售这种商品每天获利w(元).
(1)求y与x之间的函数表达式;
(2)求w与x之间的函数表达式;
(3)该商场规定这种商品每件售价不低于进价且不高于38元,要想每天获得600元的利润,每件商品的售价应定为多少元?
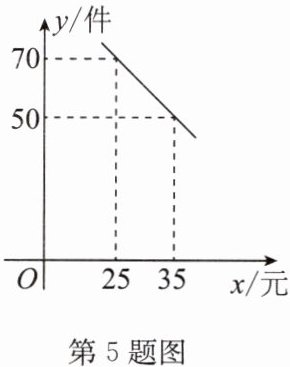
(1)求y与x之间的函数表达式;
(2)求w与x之间的函数表达式;
(3)该商场规定这种商品每件售价不低于进价且不高于38元,要想每天获得600元的利润,每件商品的售价应定为多少元?

答案:
(1)设y与x之间的函数表达式为y=kx+b(k≠0),由所给函数图像可知$\begin{cases}25k + b = 70\\35k + b = 50\end{cases}$,解得$\begin{cases}k = -2\\b = 120\end{cases}$,故y与x之间的函数表达式为y=−2x+120.
(2)
∵y=−2x+120,
∴w=(x−20)y=(x−20)(−2x+120)=−2x²+160x−2400.即w与x之间的函数表达式为w=−2x²+160x−2400.
(3)根据题意,得600=−2x²+160x−2400,解得x1=30,x2=50,
∵20 ≤ x ≤ 38,
∴x=30.答:每件商品的售价应定为30元.
(1)设y与x之间的函数表达式为y=kx+b(k≠0),由所给函数图像可知$\begin{cases}25k + b = 70\\35k + b = 50\end{cases}$,解得$\begin{cases}k = -2\\b = 120\end{cases}$,故y与x之间的函数表达式为y=−2x+120.
(2)
∵y=−2x+120,
∴w=(x−20)y=(x−20)(−2x+120)=−2x²+160x−2400.即w与x之间的函数表达式为w=−2x²+160x−2400.
(3)根据题意,得600=−2x²+160x−2400,解得x1=30,x2=50,
∵20 ≤ x ≤ 38,
∴x=30.答:每件商品的售价应定为30元.
查看更多完整答案,请扫码查看


