第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
7. 如图,$\odot O$的半径是8,$AB是\odot O$的直径,$M为AB$上一动点,$\overset{\frown}{AC}= \overset{\frown}{CD}= \overset{\frown}{BD}$,则$CM + DM$的最小值为
16
.
答案:
16
8. 已知$\odot O$的直径为10,弦$AB = 6$,$P是弦AB$上一动点,则$OP$的取值范围是
$4 \leqslant OP \leqslant 5$
.
答案:
$4 \leqslant OP \leqslant 5$
9. (2024·赣榆区期中)如图,$P是\odot O$内一定点.
(1)过点$P作弦AB$,使$P是AB$的中点.(不写作法,保留作图痕迹)
(2)若$\odot O$的半径为13,$OP = 5$,
①求过点$P的弦的长度m$的取值范围;
②过点$P$的弦中,长度为整数的弦有______条.

(1)过点$P作弦AB$,使$P是AB$的中点.(不写作法,保留作图痕迹)
(2)若$\odot O$的半径为13,$OP = 5$,
①求过点$P的弦的长度m$的取值范围;
②过点$P$的弦中,长度为整数的弦有______条.

答案:
(1)解:如答图,连接 $OP$ 并延长,过点 $P$ 作 $AB \perp OP$,则弦 $AB$ 即为所求。

(2)①解:过点 $P$ 的所有弦中,直径最长,为 26。与 $OP$ 垂直的弦最短,连接 $OA$,如答图。$\because OP \perp AB$,$\therefore AP = BP = \sqrt {OA ^ { 2 } - OP ^ { 2 }} = \sqrt {13 ^ { 2 } - 5 ^ { 2 }} = 12$,$\therefore AB = 2AP = 24$,$\therefore$ 过点 $P$ 的弦的长度 $m$ 的取值范围为 $24 \leqslant m \leqslant 26$。
②4
(1)解:如答图,连接 $OP$ 并延长,过点 $P$ 作 $AB \perp OP$,则弦 $AB$ 即为所求。

(2)①解:过点 $P$ 的所有弦中,直径最长,为 26。与 $OP$ 垂直的弦最短,连接 $OA$,如答图。$\because OP \perp AB$,$\therefore AP = BP = \sqrt {OA ^ { 2 } - OP ^ { 2 }} = \sqrt {13 ^ { 2 } - 5 ^ { 2 }} = 12$,$\therefore AB = 2AP = 24$,$\therefore$ 过点 $P$ 的弦的长度 $m$ 的取值范围为 $24 \leqslant m \leqslant 26$。
②4
10. (2024·淮安区期中)如图,某地有一座圆弧形拱桥,桥下水面宽度$AB$为24m,拱顶高出水面8m(即$CD = 8m$),$OC\perp AB$.
(1)求该圆弧形拱桥所在圆的半径;
(2)现有一艘宽10m,船舱顶部为长方形,且高出水面7.5m的货船要经过这里,此货船能顺利通过这座桥吗?
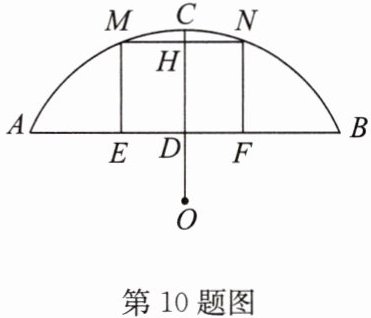
(1)求该圆弧形拱桥所在圆的半径;
(2)现有一艘宽10m,船舱顶部为长方形,且高出水面7.5m的货船要经过这里,此货船能顺利通过这座桥吗?

答案:
解:
(1)连接 $OA$,如答图。

$\because AB = 24m$,$OC \perp AB$,$\therefore AD = \frac {1} {2}AB = 12m$。设 $OA = OC = rm$,$\because CD = 8m$,$\therefore OD = (r - 8)m$。在 $Rt\triangle AOD$ 中,根据勾股定理,得 $AD ^ { 2 } + OD ^ { 2 } = OA ^ { 2 }$,即 $12 ^ { 2 } + (r - 8) ^ { 2 } = r ^ { 2 }$,解得 $r = 13$。答:该圆弧形拱桥所在圆的半径为 $13m$。
(2) $\because r = 13m$,$CD = 8m$,$\therefore OD = OC - CD = 5m$。如答图,连接 $OM$,当 $EF = MN = 10m$ 时,$\because OC \perp AB$,$\therefore OC \perp MN$,$\therefore MH = \frac {1} {2}MN = 5m$。根据勾股定理,得 $OH = \sqrt {OM ^ { 2 } - MH ^ { 2 }} = \sqrt {13 ^ { 2 } - 5 ^ { 2 }} = 12 (m)$,$\therefore DH = OH - OD = 12 - 5 = 7 (m)$。$\because 7 < 7.5$,$\therefore$ 此货船不能顺利通过这座桥。
解:
(1)连接 $OA$,如答图。

$\because AB = 24m$,$OC \perp AB$,$\therefore AD = \frac {1} {2}AB = 12m$。设 $OA = OC = rm$,$\because CD = 8m$,$\therefore OD = (r - 8)m$。在 $Rt\triangle AOD$ 中,根据勾股定理,得 $AD ^ { 2 } + OD ^ { 2 } = OA ^ { 2 }$,即 $12 ^ { 2 } + (r - 8) ^ { 2 } = r ^ { 2 }$,解得 $r = 13$。答:该圆弧形拱桥所在圆的半径为 $13m$。
(2) $\because r = 13m$,$CD = 8m$,$\therefore OD = OC - CD = 5m$。如答图,连接 $OM$,当 $EF = MN = 10m$ 时,$\because OC \perp AB$,$\therefore OC \perp MN$,$\therefore MH = \frac {1} {2}MN = 5m$。根据勾股定理,得 $OH = \sqrt {OM ^ { 2 } - MH ^ { 2 }} = \sqrt {13 ^ { 2 } - 5 ^ { 2 }} = 12 (m)$,$\therefore DH = OH - OD = 12 - 5 = 7 (m)$。$\because 7 < 7.5$,$\therefore$ 此货船不能顺利通过这座桥。
查看更多完整答案,请扫码查看


