《2025年启东中学作业本九年级数学上册苏科版连淮专版》

1. (2024·惠山区一模)如图,AB是半圆O的直径,C,D是半圆上的两点,若∠ADC= 106°,则∠CAB的度数为 (C)

A.32°
B.28°
C.16°
D.14°

答案： C

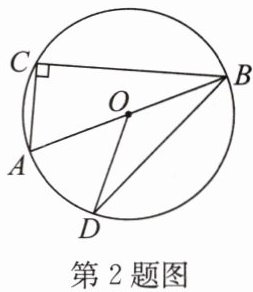
2. (2024·泰安)如图,AB是⊙O的直径,C,D是⊙O上两点,BA平分∠CBD,若∠AOD= 50°,则∠A的度数为 (A)

A.65°
B.55°
C.50°
D.75°

答案： A

3. 如图,在△ABC中,AB= AC.以AB为直径作半圆O,交BC于点D.若∠BAC= 40°,则$\overparen{AD}$的度数是$140^{\circ}$.

答案： $140^{\circ}$

4. 一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,若测得AB= 12 cm,BC= 5 cm,则圆形镜面的半径为$\frac{13}{2}\mathrm{~cm}$.

答案： $\frac{13}{2}\mathrm{~cm}$

5. 如图,AB是半圆O的直径,C,D是半圆上的两点,且\overparen{BC}的度数为20°, \overparen{AD}= \overparen{CD},求∠BCD的度数.

答案： 1. 首先，连接$AC$：
因为$AB$是半圆$O$的直径，所以$\angle ACB = 90^{\circ}$（直径所对的圆周角是直角）。
已知$\overset{\frown}{BC}$的度数为$20^{\circ}$，根据圆周角定理：同弧所对的圆周角等于弧的度数的一半，所以$\angle BAC=\frac{1}{2}\overset{\frown}{BC}$的度数，即$\angle BAC = 10^{\circ}$。
2. 然后，求$\overset{\frown}{AD}$和$\overset{\frown}{CD}$的度数：
因为$\overset{\frown}{AD}+\overset{\frown}{CD}+\overset{\frown}{BC}=180^{\circ}$（半圆的弧长对应的圆心角是$180^{\circ}$），且$\overset{\frown}{AD}=\overset{\frown}{CD}$，$\overset{\frown}{BC}$的度数为$20^{\circ}$。
设$\overset{\frown}{AD}$的度数为$x$，则$\overset{\frown}{CD}$的度数也为$x$，可得方程$x + x+20^{\circ}=180^{\circ}$。
解方程$2x=180^{\circ}-20^{\circ}=160^{\circ}$，解得$x = 80^{\circ}$。
3. 最后，求$\angle BCD$的度数：
根据圆周角定理：$\angle CAD=\frac{1}{2}\overset{\frown}{CD}$的度数，$\angle ACD=\frac{1}{2}\overset{\frown}{AD}$的度数，因为$\overset{\frown}{AD}=\overset{\frown}{CD}$，所以$\angle CAD=\angle ACD$，且$\angle CAD=\angle ACD = 40^{\circ}$。
又因为$\angle BCD=\angle ACB+\angle ACD$。
把$\angle ACB = 90^{\circ}$，$\angle ACD = 40^{\circ}$代入可得$\angle BCD=90^{\circ}+40^{\circ}=130^{\circ}$。
所以$\angle BCD$的度数是$130^{\circ}$。

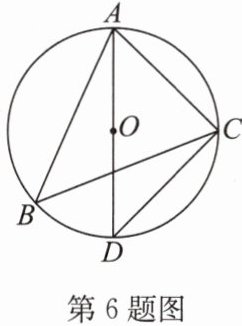
6. (2024·张家港模拟)如图,△ABC内接于⊙O,AD是⊙O的直径.若∠CAD= ∠B,AD= 8,则AC的长为 (B)

A.5
B.$4\sqrt{2}$
C.$5\sqrt{2}$
D.$4\sqrt{3}$

答案： B

7. 如图,在Rt△ABC中,∠ABC= 90°,∠A= 32°,点B,C在⊙O上,边AB,AC分别交⊙O于D,E两点,B是$\overparen{CD}$的中点,则∠ABE= ______13°.

答案： $13^{\circ}$

8. (2024·盐城月考)如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知BC= 6,∠BAC+∠EAD= 180°,则圆心A到DE的距离等于______3.

答案： 3