《2025年启东中学作业本九年级数学上册苏科版连淮专版》

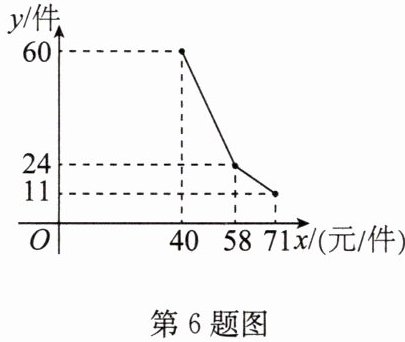
6. 某店代理某品牌商品的销售,已知该品牌商品进价为每件40元,日销售量y(件)与销售价x(元/件)之间的关系如图所示(实线),该店支付员工的工资为每人每天100元,每天还应支付其他费用150元.
(1)求日销售量y(件)与销售价x(元/件)之间的函数表达式；
(2)该店员工共3人,若某天收支恰好平衡(收入= 支出),求当天的销售价.

答案：
(1)当40 ≤ x ≤ 58时，设y与x之间的函数表达式为y=kx+b(k≠0),将(40,60),(58,24)代入,得$\begin{cases}40k + b = 60\\58k + b = 24\end{cases}$，解得$\begin{cases}k = -2\\b = 140\end{cases}$，
∴当40 ≤ x ≤ 58时，y与x之间的函数表达式为y=−2x+140;同理可得，当58 ＜ x ≤ 71时,y与x之间的函数表达式为y=−x+82.综上,y与x之间的函数表达式为$y = \begin{cases}-2x + 140(40 ≤ x ≤ 58)\\-x + 82(58 ＜ x ≤ 71)\end{cases}$。
(2)设当天的销售价为x元/件时，收支恰好平衡.当40 ≤ x ≤ 58时,根据题意,得(x−40)(−2x+140)=100×3+150,解得x1=x2=55;当58 ＜ x ≤ 71时,根据题意，得(x−40)(−x+82)=100×3+150,此方程无解.答:当天的销售价为55元/件时，收支恰好平衡.

7. 如图,在平行四边形ABCD中,AD= 2,AB= $\sqrt{6}$,∠B是锐角,AE⊥BC于点E,F是AB的中点,连接DF,EF. 若∠EFD= 90°,求AE的长.

答案： 解:如答图，延长EF交DA的延长线于点Q，连接DE，设BE=x.
∵四边形ABCD是平行四边形，
∴DQ//BC,
∴∠Q=∠BEF;
∵F是AB的中点，
∴AF=FB.又
∵∠AFQ=∠BFE,
∴△QFA≌△EFB(AAS),
∴QF=EF,AQ=BE=x.
∵∠EFD=90°,
∴DF⊥QE,
∴DQ=DE=x+2.
∵AE⊥BC,BC//AD,
∴AE⊥AD,
∴∠AEB=∠EAD=90°.
∵AE²=DE²−AD²=AB²−BE²,
∴(x+2)²−2²=($\sqrt{6}$)²−x²,整理,得x²+2x−3=0,解得x=1或x=−3(舍去),
∴BE=1,
∴AE=√AB²−BE²=$\sqrt{(\sqrt{6})² - 1²}$=$\sqrt{5}$.

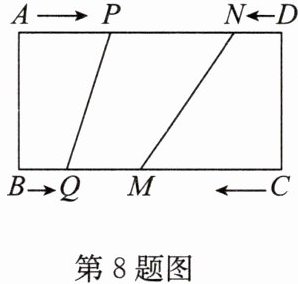
8. (2024·清江浦区期中)如图,在矩形ABCD中,BC= 20 cm,点P,Q,M,N分别同时从点A,B,C,D出发,沿AD,BC,CB,DA方向在矩形的边上运动,当有一个点先到达所在边的另一个端点时,运动即停止. 已知在相同时间内,若BQ= x cm(x≠0),则$AP= 2x cm,CM= 3x cm,DN= x^2 cm.$
(1)当x为何值时,点P,N重合；
(2)当x为何值时,以P,Q,M,N为顶点的四边形是平行四边形.

答案：
(1)
∵点P,N重合,
∴2x+x²=20,解得x1=$\sqrt{21}$−1,x2=−$\sqrt{21}$−1(舍去).
∴当x=$\sqrt{21}$−1时，点P,N重合.
(2)因为当点N到达点A时,x=2$\sqrt{5}$,此时点M和点Q 还未相遇，所以点Q只能在点M的左侧.①当点P在点N的左侧时，依题意，得20−(x+3x)=20−(2x+x²),解得x1=0(舍去),x2=2.当x=2时，四边形PQMN是平行四边形;②当点P在点N的右侧时，依题意，得20−(x+3x)=(2x+x²)−20,解得x1=−10(舍去),x2=4.当x=4时，四边形NQMP是平行四边形.综上,当x=2或x=4时,以P,Q,M,N为顶点的四边形是平行四边形.