《2025年启东中学作业本九年级数学上册苏科版连淮专版》

7. 如果一个矩形经过一个多边形的各顶点,那么我们把这个矩形叫做这个多边形的外接矩形,如图,矩形ABCD是正六边形EFGHPQ的外接矩形,如果正六边形EFGHPQ的边长为2,那么矩形ABCD的长边与短边的比是 (A)
A.$2:\sqrt {3}$
B.$2:\sqrt {2}$
C.$3:\sqrt {3}$
D.$\sqrt {3}:1$

答案： A

8. 数学文化(2024·丹阳二模)刘徽是我国魏晋时期卓越的数学家,他在《九章算术注》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积. 如图,若用圆(半径为r)的内接正八边形的面积来估计这个圆的面积,则估计值比圆的实际面积少$ ( \pi - 2 \sqrt { 2 } ) r ^ { 2 } $.(用含r的代数式表示)

答案： $ ( \pi - 2 \sqrt { 2 } ) r ^ { 2 } $

9. 如图,AE是$\odot O$的直径,用直尺和圆规作$\odot O$的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).

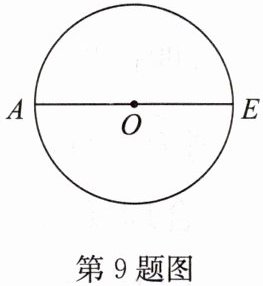
答案：
解:正八边形 $ A B C D E F G H $ 如答图所示.
　　　　　　　　

10. (2024·崇川区月考)(1)如图①,$\triangle ABC是\odot O$的内接正三角形,P为劣弧BC上一动点,求证:$PA= PB+PC;$
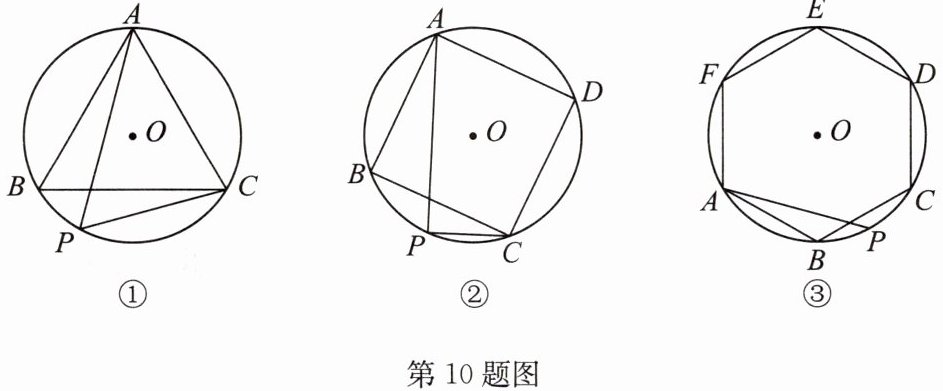
(2)如图②,四边形ABCD是$\odot O$的内接正方形,P为劣弧BC上一动点,求证:$PA= PC+\sqrt {2}PB;$
(3)如图③,六边形ABCDEF是$\odot O$的内接正六边形,P为劣弧BC上一动点,则PA,PB,PC三者之间的关系为______.

答案：
10.
(1)证明:延长 $ B P $ 至点 $ E $, 使 $ P E = P C $, 连接 $ C E $, 如答图①,
　　　　　　　　
$ \because \triangle A B C $ 是 $ \odot O $ 的内接正三角形,
$ \therefore \angle B A C = \angle A C B = 60 ^ { \circ } $.
$ \because A, B, P, C $ 四点共圆, $ \therefore \angle B A C + \angle B P C = 180 ^ { \circ } $.
$ \because \angle B P C + \angle E P C = 180 ^ { \circ } $,
$ \therefore \angle B A C = \angle C P E = 60 ^ { \circ } $.
又 $ \because P E = P C, \therefore \triangle P C E $ 是等边三角形,
$ \therefore C E = P C, \angle E = \angle P C E = 60 ^ { \circ } $.
又 $ \because \angle B C E = 60 ^ { \circ } + \angle B C P, \angle A C P = 60 ^ { \circ } + \angle B C P $,
$ \therefore \angle B C E = \angle A C P $.
$ \because \triangle A B C $ 与 $ \triangle E C P $ 均为等边三角形,
$ \therefore C E = P C, A C = B C $.
在 $ \triangle B E C $ 和 $ \triangle A P C $ 中, $ \left\{ \begin{array} { l } { C E = C P }, \\ { \angle B C E = \angle A C P }, \\ { B C = A C }, \end{array} \right. $
$ \therefore \triangle B E C \cong \triangle A P C ( S A S ) $,
$ \therefore P A = B E = P B + P E = P B + P C $.
(2)证明:连接 $ B P $, 过点 $ B $ 作 $ B E \perp P B $ 交 $ P A $ 于点 $ E $, 如答图②.
　　　　　　　
$ \because $ 四边形 $ A B C D $ 是 $ \odot O $ 的内接正方形,
$ \therefore \angle A B C = 90 ^ { \circ }, A B = B C $.
$ \because \angle 1 + \angle 2 = \angle 2 + \angle 3 = 90 ^ { \circ }, \therefore \angle 1 = \angle 3 $.
易知 $ \angle A P B = 45 ^ { \circ }, \therefore B P = B E, \therefore P E = \sqrt { 2 } P B $.
在 $ \triangle A B E $ 和 $ \triangle C B P $ 中, $ \left\{ \begin{array} { l } { B E = B P }, \\ { \angle 1 = \angle 3 }, \\ { A B = C B }, \end{array} \right. $
$ \therefore \triangle A B E \cong \triangle C B P ( S A S ) $,
$ \therefore P C = A E, \therefore P A = A E + P E = P C + \sqrt { 2 } P B $.
(3) $ P A = P C + \sqrt { 3 } P B $