《2025年启东中学作业本九年级数学上册苏科版连淮专版》

10. 如图①,圆锥的母线长$l= 16$ cm,若以顶点O为中心,将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角$\theta=270^{\circ}$.求:
(1)圆锥的底面圆的半径;
(2)圆锥的表面积.(结果保留π)

答案： 解：
(1)设底面圆的半径为 $r\ cm$，由题意，得 $3 × 2\pi r = \frac{270 × \pi × 16}{180}$，解得 $r = 4$，即圆锥的底面圆的半径为 $4\ cm$。
(2)圆锥的表面积为 $\pi × 4^2 + \frac{1}{2} × 2\pi × 4 × 16 = 80\pi (cm^2)$。

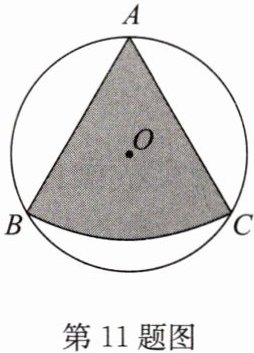
11. 如图,在半径为$\sqrt{3}$的圆形纸片中,剪出一个圆心角为$60^{\circ}$的扇形(图中的阴影部分).
(1)求这个扇形的半径;
(2)若用剪得的扇形纸片围成一个圆锥的侧面,求所围成圆锥的底面圆的半径.

答案：
解：
(1)如答图，连接 $BC$，$OB$，$OC$，过点 $O$ 作 $OD \perp BC$，垂足为 $D$。 $\because \angle BAC = 60^{\circ}$，$OB = OC = \sqrt{3}$，$AB = AC$，$\therefore \angle BOC = 120^{\circ}$，$\angle OBC = \angle OCB = 30^{\circ}$，$\triangle ABC$ 是等边三角形。$\therefore BC = 2BD = 2 × \sqrt{(\sqrt{3})^2 - (\frac{\sqrt{3}}{2})^2} = 3$，$AB = BC = AC$。$\therefore$ 这个扇形的半径为 $3$。
(2)设圆锥底面圆的半径为 $r$，根据题意，得 $\frac{60 × \pi × 3}{180} = 2\pi r$，解得 $r = \frac{1}{2}$。故所围成圆锥的底面圆的半径为 $\frac{1}{2}$。

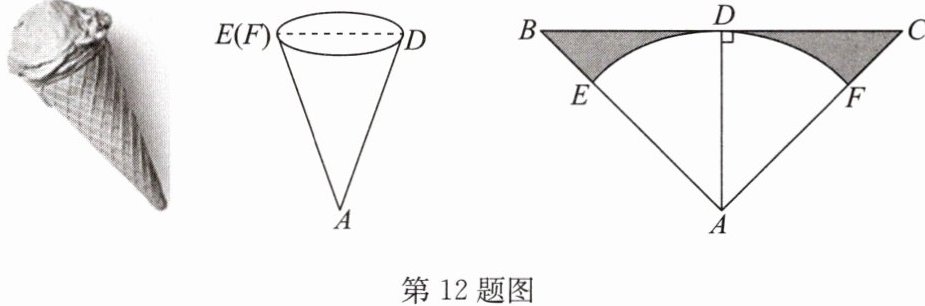
12. 某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED与母线AD的长度之比为$1:2$.制作这种外包装需要用如图所示的等腰三角形材料,其中$AB= AC,AD⊥BC$.将扇形AEF围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角$∠BAC$的度数;
(2)若圆锥底面圆的直径ED为5 cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)

答案： 解：
(1)设 $\angle BAC = n^{\circ}$。由题意，得 $\pi \cdot DE = \frac{n\pi \cdot AD}{180}$，$AD = 2DE$，解得 $n = 90$，$\therefore \angle BAC = 90^{\circ}$。
(2) $\because AB = AC$，$\angle BAC = 90^{\circ}$，$AD \perp BC$，$\therefore DB = DC = AD$，$\therefore BC = 2AD$。$\because AD = 2DE = 10\ cm$，$\therefore S_{阴影} = \frac{1}{2}BC \cdot AD - S_{扇形AEF} = \frac{1}{2} × 20 × 10 - \frac{90\pi × 10^2}{360} = (100 - 25\pi) cm^2$。