第95页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
3.某射击队从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
| |第一次|第二次|第三次|第四次|第五次|第六次|平均成绩|中位数|
|甲|10|8|9|8|10|9|9|①|
|乙|10|7|10|10|9|8|②|9.5|
(1)写出表中①,②表示的数:①
(2)请分别计算甲、乙两人六次测试成绩的方差;
(3)你认为推荐谁参加比赛更合适? 并说明理由.
| |第一次|第二次|第三次|第四次|第五次|第六次|平均成绩|中位数|
|甲|10|8|9|8|10|9|9|①|
|乙|10|7|10|10|9|8|②|9.5|
(1)写出表中①,②表示的数:①
9
,②9
;(2)请分别计算甲、乙两人六次测试成绩的方差;
解: 甲六次测试成绩的方差为 $\frac{1}{6}×[2×(10 - 9)^2 + 2×(9 - 9)^2 + 2×(8 - 9)^2] = \frac{2}{3}$;
乙六次测试成绩的方差为 $\frac{1}{6}×[3×(10 - 9)^2 + (9 - 9)^2 + (8 - 9)^2 + (7 - 9)^2] = \frac{4}{3}$.
乙六次测试成绩的方差为 $\frac{1}{6}×[3×(10 - 9)^2 + (9 - 9)^2 + (8 - 9)^2 + (7 - 9)^2] = \frac{4}{3}$.
(3)你认为推荐谁参加比赛更合适? 并说明理由.
解: 推荐甲参加比赛更合适. 理由如下:
∵ 甲、乙的平均成绩相同, 而甲成绩的方差小于乙成绩的方差,
∴ 甲的成绩更稳定,
故推荐甲参加比赛更合适. (答案不唯一, 合理即可)
∵ 甲、乙的平均成绩相同, 而甲成绩的方差小于乙成绩的方差,
∴ 甲的成绩更稳定,
故推荐甲参加比赛更合适. (答案不唯一, 合理即可)
答案:
3.
(1) 9 9
(2) 解: 甲六次测试成绩的方差为 $\frac{1}{6}×[2×(10 - 9)^2 + 2×(9 - 9)^2 + 2×(8 - 9)^2] = \frac{2}{3}$;
乙六次测试成绩的方差为 $\frac{1}{6}×[3×(10 - 9)^2 + (9 - 9)^2 + (8 - 9)^2 + (7 - 9)^2] = \frac{4}{3}$.
(3) 解: 推荐甲参加比赛更合适. 理由如下:
∵ 甲、乙的平均成绩相同, 而甲成绩的方差小于乙成绩的方差,
∴ 甲的成绩更稳定,
故推荐甲参加比赛更合适. (答案不唯一, 合理即可)
(1) 9 9
(2) 解: 甲六次测试成绩的方差为 $\frac{1}{6}×[2×(10 - 9)^2 + 2×(9 - 9)^2 + 2×(8 - 9)^2] = \frac{2}{3}$;
乙六次测试成绩的方差为 $\frac{1}{6}×[3×(10 - 9)^2 + (9 - 9)^2 + (8 - 9)^2 + (7 - 9)^2] = \frac{4}{3}$.
(3) 解: 推荐甲参加比赛更合适. 理由如下:
∵ 甲、乙的平均成绩相同, 而甲成绩的方差小于乙成绩的方差,
∴ 甲的成绩更稳定,
故推荐甲参加比赛更合适. (答案不唯一, 合理即可)
4.(2024·高港区三模)某校举办“跨学科综合实践活动”,五名评委对每组同学的参赛作品进行打分.对参加比赛的甲、乙、丙三个组参赛作品得分(单位:分)的数据进行整理、描述和分析,下面给出了部分信息.
A.甲、丙两组参赛作品得分的折线图如图;
B.在给乙组参赛作品的打分时,其中三位评委打分分别为87,93,95,其余两位评委的打分均高于85;
C.甲、乙、丙三个组参赛作品得分的平均数如下表:
|甲组|乙组|丙组|
|88|90|n|
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)若某组参赛作品评委打分的5个数据的方差越小,则认为评委对该组参赛作品的评价越“一致”.据此推断:对于甲、丙两组的参赛作品,五位评委评价更“一致”的是
(3)该校现准备推荐一个小组的作品到区里参加比赛,你认为应该推荐哪个小组? 请说明理由.
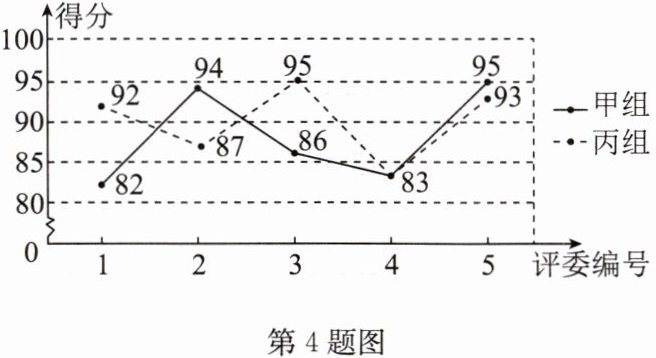
A.甲、丙两组参赛作品得分的折线图如图;
B.在给乙组参赛作品的打分时,其中三位评委打分分别为87,93,95,其余两位评委的打分均高于85;
C.甲、乙、丙三个组参赛作品得分的平均数如下表:
|甲组|乙组|丙组|
|88|90|n|
根据以上信息,回答下列问题:
(1)写出表中n的值;
90
(2)若某组参赛作品评委打分的5个数据的方差越小,则认为评委对该组参赛作品的评价越“一致”.据此推断:对于甲、丙两组的参赛作品,五位评委评价更“一致”的是
丙
组;(填“甲”或“丙”)(3)该校现准备推荐一个小组的作品到区里参加比赛,你认为应该推荐哪个小组? 请说明理由.
解: 应该推荐乙组. 理由如下: 乙组和丙组的平均成绩都是 90 分, 高于甲组的 88 分, 而乙组其余两位评委打分均高于 85 分, 可以推测乙组成绩较为稳定, 故推荐乙组. (答案不唯一, 合理即可)

答案:
4.
(1) 解: 由题意, 得 $n = \frac{92 + 87 + 95 + 83 + 93}{5} = 90$.
(2) 丙
(3) 解: 应该推荐乙组. 理由如下: 乙组和丙组的平均成绩都是 90 分, 高于甲组的 88 分, 而乙组其余两位评委打分均高于 85 分, 可以推测乙组成绩较为稳定, 故推荐乙组. (答案不唯一, 合理即可)
(1) 解: 由题意, 得 $n = \frac{92 + 87 + 95 + 83 + 93}{5} = 90$.
(2) 丙
(3) 解: 应该推荐乙组. 理由如下: 乙组和丙组的平均成绩都是 90 分, 高于甲组的 88 分, 而乙组其余两位评委打分均高于 85 分, 可以推测乙组成绩较为稳定, 故推荐乙组. (答案不唯一, 合理即可)
查看更多完整答案,请扫码查看


