《2025年启东中学作业本九年级数学上册苏科版连淮专版》

12.(10分)已知关于x的一元二次方程$(a-1)x^{2}+(2a+1)x+2= 0$.
(1)求证：此方程一定有两个不相等的实数根；
(2)如果这个方程根的判别式的值等于9,求a的值.

答案：
(1) 证明：$ (2a + 1)^{2} - 8(a - 1) $ $ = 4a^{2} + 4a + 1 - 8a + 8 $ $ = 4a^{2} - 4a + 1 + 8 $ $ = (2a - 1)^{2} + 8 $，$ \because (2a - 1)^{2} \geq 0 $，$ \therefore (2a - 1)^{2} + 8 ＞ 0 $，$ \therefore $ 此方程一定有两个不相等的实数根。
(2) 解：$ \because (2a - 1)^{2} + 8 = 9 $，$ \therefore (2a - 1)^{2} = 1 $，解得 $ a_{1} = 0 $，$ a_{2} = 1 $。$ \because a \neq 1 $，$ \therefore a = 0 $。

13.(12分)某学校计划利用一片空地为学生建一个面积为$80m^{2}$的矩形车棚,其中一面靠墙(墙的可用长度为12m),已知现有的木板材料可使新建板墙的总长为26m.
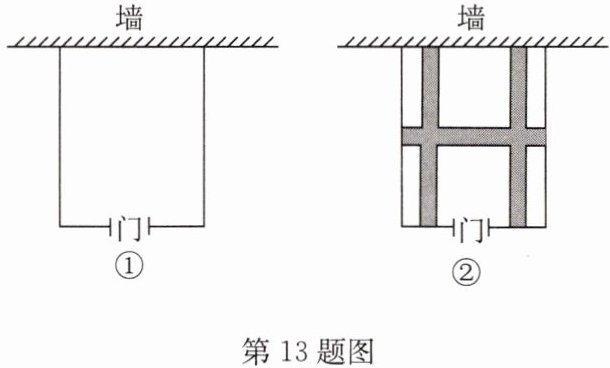
(1)根据学校的要求,在与墙平行的一面开一个2m宽的门(如图①),那么这个矩形车棚相邻两边长分别为多少米？
(2)如图②,为了方便学生取车,施工单位决定在车棚内修建3条等宽的小路,使得停放自行车的面积为$54m^{2}$,那么小路的宽度为多少米？

答案：
(1) 设与墙垂直的一边长为 $ x $ m，则与墙平行的一边长为 $ (26 + 2 - 2x) $ m，根据题意，得 $ x(26 + 2 - 2x) = 80 $，整理，得 $ x^{2} - 14x + 40 = 0 $，解得 $ x_{1} = 4 $，$ x_{2} = 10 $，当 $ x = 4 $ 时，$ 26 + 2 - 2x = 26 + 2 - 2×4 = 20 ＞ 12 $，不符合题意，舍去；当 $ x = 10 $ 时，$ 26 + 2 - 2x = 26 + 2 - 2×10 = 8 ＜ 12 $，符合题意。答：这个矩形车棚相邻两边长分别为 10 m，8 m。
(2) 设小路的宽度为 $ y $ m，则剩余部分可合成长为 $ (10 - y) $ m，宽为 $ (8 - 2y) $ m 的矩形，根据题意，得 $ (10 - y)(8 - 2y) = 54 $，整理，得 $ y^{2} - 14y + 13 = 0 $，解得 $ y_{1} = 1 $，$ y_{2} = 13 $（不符合题意，舍去）。答：小路的宽度为 1 m。

14.(13分)新定义(2024·镇江月考)如果关于x的一元二次方程$ax^{2}+bx+c= 0(a≠0)$有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”. 例如,一元二次方程$x^{2}-6x+8= 0$的两个根是2和4,则方程$x^{2}-6x+8= 0$就是“倍根方程”.
(1)若一元二次方程$x^{2}-3x+c= 0$是“倍根方程”,求c的值；
(2)若$(x-2)(mx-n)= 0(m≠0)$是“倍根方程”,求代数式$4m^{2}-5mn+n^{2}$的值；
(3)若关于x的一元二次方程$ax^{2}+bx+c= 0(a≠0)$是“倍根方程”,请说明：$2b^{2}= 9ac$.

答案：
(1) 设一元二次方程 $ x^{2} - 3x + c = 0 $ 的一个根为 $ x_{1} $，另一个根为 $ 2x_{1} $，由根与系数的关系，得 $ x_{1} + 2x_{1} = 3 $，$ \therefore x_{1} = 1 $，即一个根为 1，而另一个根为 2，$ \therefore c = 1×2 = 2 $。
(2) 方程 $ (x - 2)(mx - n) = 0 $ 的一个根为 2，则另一个根为 1 或 4，当另一个根为 1 时，则 $ -1×(m - n) = 0 $，$ \therefore m - n = 0 $，当另一个根为 4 时，则 $ 2×(4m - n) = 0 $，$ \therefore 4m - n = 0 $。$ \therefore 4m^{2} - 5mn + n^{2} = (m - n)(4m - n) = 0 $。
(3) 由求根公式得 $ x_{1} = \frac{-b + \sqrt{b^{2} - 4ac}}{2a} $，$ x_{2} = \frac{-b - \sqrt{b^{2} - 4ac}}{2a} $，若 $ x_{1} = 2x_{2} $，则 $ \frac{-b + \sqrt{b^{2} - 4ac}}{2a} = \frac{-b - \sqrt{b^{2} - 4ac}}{2a} × 2 $，化简，得 $ 2b^{2} = 9ac $。若 $ 2x_{1} = x_{2} $，则 $ \frac{-b + \sqrt{b^{2} - 4ac}}{2a} × 2 = \frac{-b - \sqrt{b^{2} - 4ac}}{2a} $，化简，得 $ 2b^{2} = 9ac $。因此，当关于 $ x $ 的一元二次方程 $ ax^{2} + bx + c = 0(a \neq 0) $ 是“倍根方程”时，总有 $ 2b^{2} = 9ac $。