第71页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
圆周角:在圆中,除圆心角外,还有一类角(如图24-1-19中的∠ACB),它的
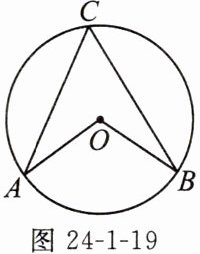
顶点
在圆上,并且两边都与圆相交
,我们把这样的角叫做圆周角.
答案:
顶点 相交
例1(教材补充例题)如图24-1-20,∠APB是圆周角的是(
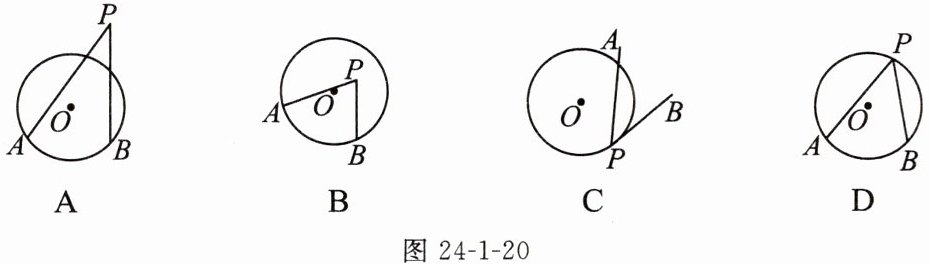
D
)
答案:
D
操作猜想
用量角器分别测量图24-1-21的各圆中$\overset{\frown}{BC}$所对的圆周角∠BAC和圆心角∠BOC的度数,填入下表,观察分析它们之间有什么关系,并用一句话表述你发现的规律.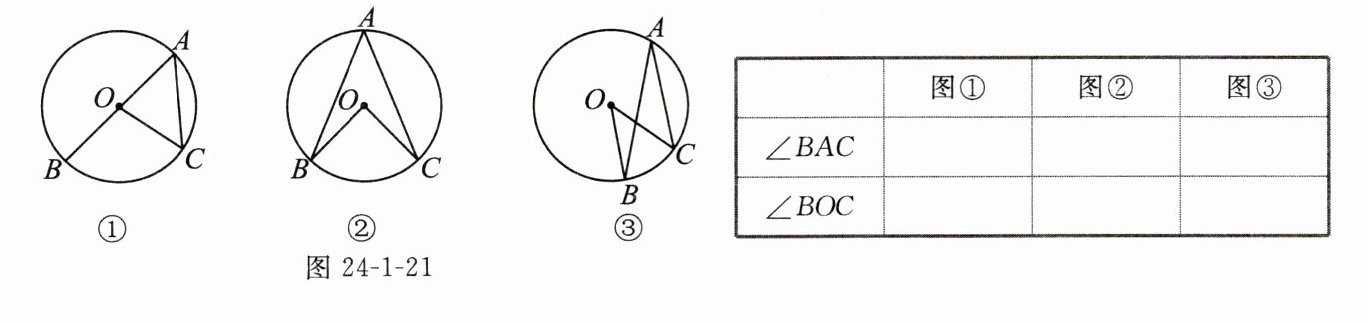
推理证明
1. 请你根据图24-1-21中的各种情况,证明你发现的规律.
证明:(1)如图①,当圆心O在∠BAC的一边上时.
(2)如图③,当圆心O在∠BAC的外部时.
2. 一条弧所对的圆心角有几个?所对的圆周角有几个?
用量角器分别测量图24-1-21的各圆中$\overset{\frown}{BC}$所对的圆周角∠BAC和圆心角∠BOC的度数,填入下表,观察分析它们之间有什么关系,并用一句话表述你发现的规律.

推理证明
1. 请你根据图24-1-21中的各种情况,证明你发现的规律.
证明:(1)如图①,当圆心O在∠BAC的一边上时.
(2)如图③,当圆心O在∠BAC的外部时.
2. 一条弧所对的圆心角有几个?所对的圆周角有几个?
答案:
证明:
(1)
∵OA=OC,
∴∠BAC=∠OCA.
又∠BOC=∠BAC+∠OCA,
∴∠BAC=$\frac{1}{2}$∠BOC.
(2) 连接AO并延长,交⊙O于点D,如图.
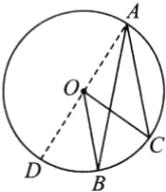
由
(1)的结论得∠BAD=$\frac{1}{2}$∠DOB, ∠CAD=$\frac{1}{2}$∠DOC,
∴∠CAD−∠BAD=$\frac{1}{2}$∠DOC−$\frac{1}{2}$∠DOB=$\frac{1}{2}$(∠DOC−∠DOB), 即∠BAC=$\frac{1}{2}$∠BOC.
2.解: 一条弧所对的圆心角有一个, 所对的圆周角有无数个.
证明:
(1)
∵OA=OC,
∴∠BAC=∠OCA.
又∠BOC=∠BAC+∠OCA,
∴∠BAC=$\frac{1}{2}$∠BOC.
(2) 连接AO并延长,交⊙O于点D,如图.

由
(1)的结论得∠BAD=$\frac{1}{2}$∠DOB, ∠CAD=$\frac{1}{2}$∠DOC,
∴∠CAD−∠BAD=$\frac{1}{2}$∠DOC−$\frac{1}{2}$∠DOB=$\frac{1}{2}$(∠DOC−∠DOB), 即∠BAC=$\frac{1}{2}$∠BOC.
2.解: 一条弧所对的圆心角有一个, 所对的圆周角有无数个.
查看更多完整答案,请扫码查看


