第55页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
中心对称的相关概念:把一个图形绕着某一点旋转
180°
,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心
(简称中心).这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点
.
答案:
[初识概念] 180° 对称中心 对称点
例1(教材补充例题)下列选项中,$△A'B'C'$与$△ABC$成中心对称的是(
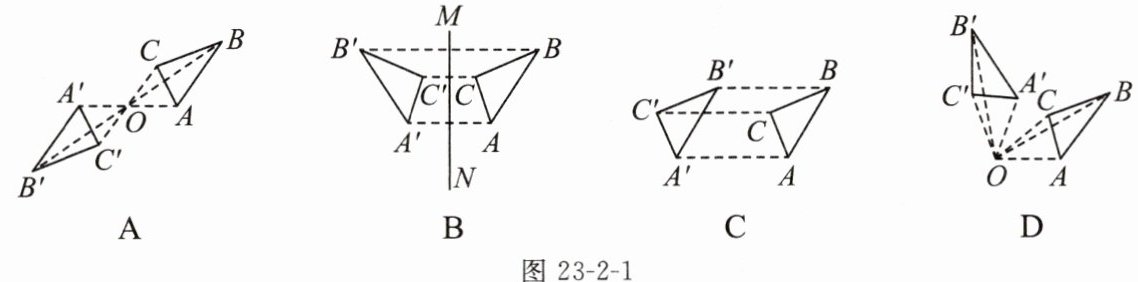
A
)
答案:
例 1 A
如图23-2-2,三角尺的一个顶点是O,以点O为中心旋转三角尺,画出$△ABC$关于点O中心对称的$△A'B'C'.$
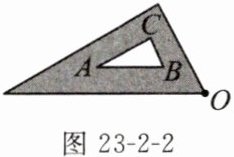

答案:
1. 首先,连接$AO$并延长$AO$到$A'$,使$OA' = OA$:
这是根据中心对称的性质,中心对称的点到对称中心的距离相等。
2. 然后,连接$BO$并延长$BO$到$B'$,使$OB' = OB$:
同样依据中心对称点的性质。
3. 接着,连接$CO$并延长$CO$到$C'$,使$OC' = OC$:
还是根据中心对称点的性质。
4. 最后,顺次连接$A'$、$B'$、$C'$:
得到$\triangle A'B'C'$,$\triangle A'B'C'$就是$\triangle ABC$关于点$O$中心对称的三角形。
综上,按照上述步骤画出$\triangle A'B'C'$。
这是根据中心对称的性质,中心对称的点到对称中心的距离相等。
2. 然后,连接$BO$并延长$BO$到$B'$,使$OB' = OB$:
同样依据中心对称点的性质。
3. 接着,连接$CO$并延长$CO$到$C'$,使$OC' = OC$:
还是根据中心对称点的性质。
4. 最后,顺次连接$A'$、$B'$、$C'$:
得到$\triangle A'B'C'$,$\triangle A'B'C'$就是$\triangle ABC$关于点$O$中心对称的三角形。
综上,按照上述步骤画出$\triangle A'B'C'$。
中心对称的性质:
(1)中心对称的两个图形,对称点所连线段都经过
(2)中心对称的两个图形是
(1)中心对称的两个图形,对称点所连线段都经过
对称中心
,而且被对称中心所平分
.(2)中心对称的两个图形是
全等图形
.
答案:
[概括新知]
(1)对称中心 平分
(2)全等图形
(1)对称中心 平分
(2)全等图形
练一练 如图23-2-3,$△ABC$与$△DEF$关于点O对称,则下列结论不正确的是(
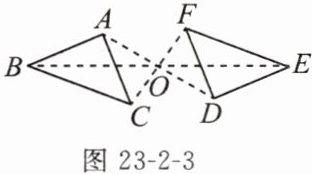
A.点A与点D是对称点
B.$∠ACB=∠DEF$
C.$BO=EO$
D.$AB// DE$
B
)
A.点A与点D是对称点
B.$∠ACB=∠DEF$
C.$BO=EO$
D.$AB// DE$
答案:
练一练 B
例2(教材典题)(1)如图23-2-4,选择点O为对称中心,画出点A关于点O的对称点$A';$
(2)如图23-2-5,选择点O为对称中心,画出与$△ABC$关于点O对称的$△A'B'C'.$

1. (1)
解:连接$AO$并延长$AO$到$A'$,使$OA' = OA$,则点$A'$就是点$A$关于点$O$的对称点。
2. (2)
解:
第一步:连接$AO$并延长$AO$到$A'$,使$OA' = OA$,得到点$A$关于点$O$的对称点$A'$;
第二步:连接$BO$并延长$BO$到$B'$,使$OB' = OB$,得到点$B$关于点$O$的对称点$B'$;
第三步:连接$CO$并延长$CO$到$C'$,使$OC' = OC$,得到点$C$关于点$O$的对称点$C'$;
第四步:连接$A'B'$,$B'C'$,$C'A'$,则$\triangle A'B'C'$就是与$\triangle ABC$关于点$O$对称的三角形。
(2)如图23-2-5,选择点O为对称中心,画出与$△ABC$关于点O对称的$△A'B'C'.$

1. (1)
解:连接$AO$并延长$AO$到$A'$,使$OA' = OA$,则点$A'$就是点$A$关于点$O$的对称点。
2. (2)
解:
第一步:连接$AO$并延长$AO$到$A'$,使$OA' = OA$,得到点$A$关于点$O$的对称点$A'$;
第二步:连接$BO$并延长$BO$到$B'$,使$OB' = OB$,得到点$B$关于点$O$的对称点$B'$;
第三步:连接$CO$并延长$CO$到$C'$,使$OC' = OC$,得到点$C$关于点$O$的对称点$C'$;
第四步:连接$A'B'$,$B'C'$,$C'A'$,则$\triangle A'B'C'$就是与$\triangle ABC$关于点$O$对称的三角形。
答案:
1. (1)
解:连接$AO$并延长$AO$到$A'$,使$OA' = OA$,则点$A'$就是点$A$关于点$O$的对称点。
2. (2)
解:
第一步:连接$AO$并延长$AO$到$A'$,使$OA' = OA$,得到点$A$关于点$O$的对称点$A'$;
第二步:连接$BO$并延长$BO$到$B'$,使$OB' = OB$,得到点$B$关于点$O$的对称点$B'$;
第三步:连接$CO$并延长$CO$到$C'$,使$OC' = OC$,得到点$C$关于点$O$的对称点$C'$;
第四步:连接$A'B'$,$B'C'$,$C'A'$,则$\triangle A'B'C'$就是与$\triangle ABC$关于点$O$对称的三角形。
解:连接$AO$并延长$AO$到$A'$,使$OA' = OA$,则点$A'$就是点$A$关于点$O$的对称点。
2. (2)
解:
第一步:连接$AO$并延长$AO$到$A'$,使$OA' = OA$,得到点$A$关于点$O$的对称点$A'$;
第二步:连接$BO$并延长$BO$到$B'$,使$OB' = OB$,得到点$B$关于点$O$的对称点$B'$;
第三步:连接$CO$并延长$CO$到$C'$,使$OC' = OC$,得到点$C$关于点$O$的对称点$C'$;
第四步:连接$A'B'$,$B'C'$,$C'A'$,则$\triangle A'B'C'$就是与$\triangle ABC$关于点$O$对称的三角形。
查看更多完整答案,请扫码查看


