第36页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
(1)你能把二次函数$y=\frac {1}{2}x^{2}-6x+21$化成$y=a(x-h)^{2}+k$的形式吗?
答案:
解:y=$\frac{1}{2}$x²−6x+21=$\frac{1}{2}$(x−6)²+3.
(2)类比以上方法将二次函数$y=ax^{2}+bx+c$化为$y=a(x-h)^{2}+k$的形式.
答案:
解:
$\begin{aligned}y&=ax^{2}+bx+c\\&=a\left(x^{2}+\frac{b}{a}x\right)+c\\&=a\left(x^{2}+\frac{b}{a}x+\frac{b^{2}}{4a^{2}}-\frac{b^{2}}{4a^{2}}\right)+c\\&=a\left(x+\frac{b}{2a}\right)^{2}+c-\frac{b^{2}}{4a}\\&=a\left(x+\frac{b}{2a}\right)^{2}+\frac{4ac - b^{2}}{4a}\end{aligned}$
其中$h = -\frac{b}{2a}$,$k=\frac{4ac - b^{2}}{4a}$。
$\begin{aligned}y&=ax^{2}+bx+c\\&=a\left(x^{2}+\frac{b}{a}x\right)+c\\&=a\left(x^{2}+\frac{b}{a}x+\frac{b^{2}}{4a^{2}}-\frac{b^{2}}{4a^{2}}\right)+c\\&=a\left(x+\frac{b}{2a}\right)^{2}+c-\frac{b^{2}}{4a}\\&=a\left(x+\frac{b}{2a}\right)^{2}+\frac{4ac - b^{2}}{4a}\end{aligned}$
其中$h = -\frac{b}{2a}$,$k=\frac{4ac - b^{2}}{4a}$。
例1(教材补充例题)把下列函数写成$y=a(x-h)^{2}+k$的形式,并写出其图象的开口方向、对称轴和顶点坐标.
(1)$y=-x^{2}+6x+1;$ (2)$y=\frac {2}{3}x^{2}-4x+\frac {19}{3}.$
(1)$y=-x^{2}+6x+1;$ (2)$y=\frac {2}{3}x^{2}-4x+\frac {19}{3}.$
答案:
解:
(1)y=-x²+6x+1=-(x-3)²+10,
∴此函数图象的开口向下,对称轴为直线x=3,顶点坐标为(3,10).
(2)y=$\frac{2}{3}$x²−4x+$\frac{19}{3}$=$\frac{2}{3}$(x−3)²+$\frac{1}{3}$,
∴此函数图象的开口向上,对称轴为直线x=3,顶点坐标为(3,$\frac{1}{3}$).
(1)y=-x²+6x+1=-(x-3)²+10,
∴此函数图象的开口向下,对称轴为直线x=3,顶点坐标为(3,10).
(2)y=$\frac{2}{3}$x²−4x+$\frac{19}{3}$=$\frac{2}{3}$(x−3)²+$\frac{1}{3}$,
∴此函数图象的开口向上,对称轴为直线x=3,顶点坐标为(3,$\frac{1}{3}$).
如何画出函数$y=\frac {1}{2}x^{2}-6x+21$的图象?说出你的方法,并在坐标系中画出图象.
答案:
解:y=$\frac{1}{2}$x²−6x+21=$\frac{1}{2}$(x−6)²+3.
列表如下:
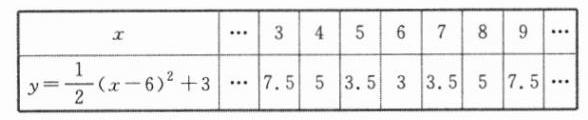
描点、连线,得到函数y=$\frac{1}{2}$(x−6)²+3的图象如图.

解:y=$\frac{1}{2}$x²−6x+21=$\frac{1}{2}$(x−6)²+3.
列表如下:

描点、连线,得到函数y=$\frac{1}{2}$(x−6)²+3的图象如图.

(1)写出二次函数$y=\frac {1}{2}x^{2}-6x+21$的图象的开口方向、对称轴和顶点坐标与函数的增减性;
答案:
解:
(1)二次函数y=$\frac{1}{2}$x²−6x+21的图象开口向上,对称轴是直线x=6,顶点坐标是(6,3).当x<6 时,y随x的增大而减小;当x>6时,y随x的增大而增大.
(1)二次函数y=$\frac{1}{2}$x²−6x+21的图象开口向上,对称轴是直线x=6,顶点坐标是(6,3).当x<6 时,y随x的增大而减小;当x>6时,y随x的增大而增大.
(2)二次函数$y=\frac {1}{2}x^{2}-6x+21$的图象是由二次函数$y=\frac {1}{2}x^{2}$的图象经过怎样的平移得到的?
答案:
(2)将二次函数y=$\frac{1}{2}$x²的图象向右平移6个单位长度,再向上平移3个单位长度,得到二次函数y=$\frac{1}{2}$x²−6x+21的图象(平移方法不唯一).
(2)将二次函数y=$\frac{1}{2}$x²的图象向右平移6个单位长度,再向上平移3个单位长度,得到二次函数y=$\frac{1}{2}$x²−6x+21的图象(平移方法不唯一).
查看更多完整答案,请扫码查看


