《2025年全品学练考九年级数学上册人教版》

二次函数$y=ax^{2}+k$的图象和性质:

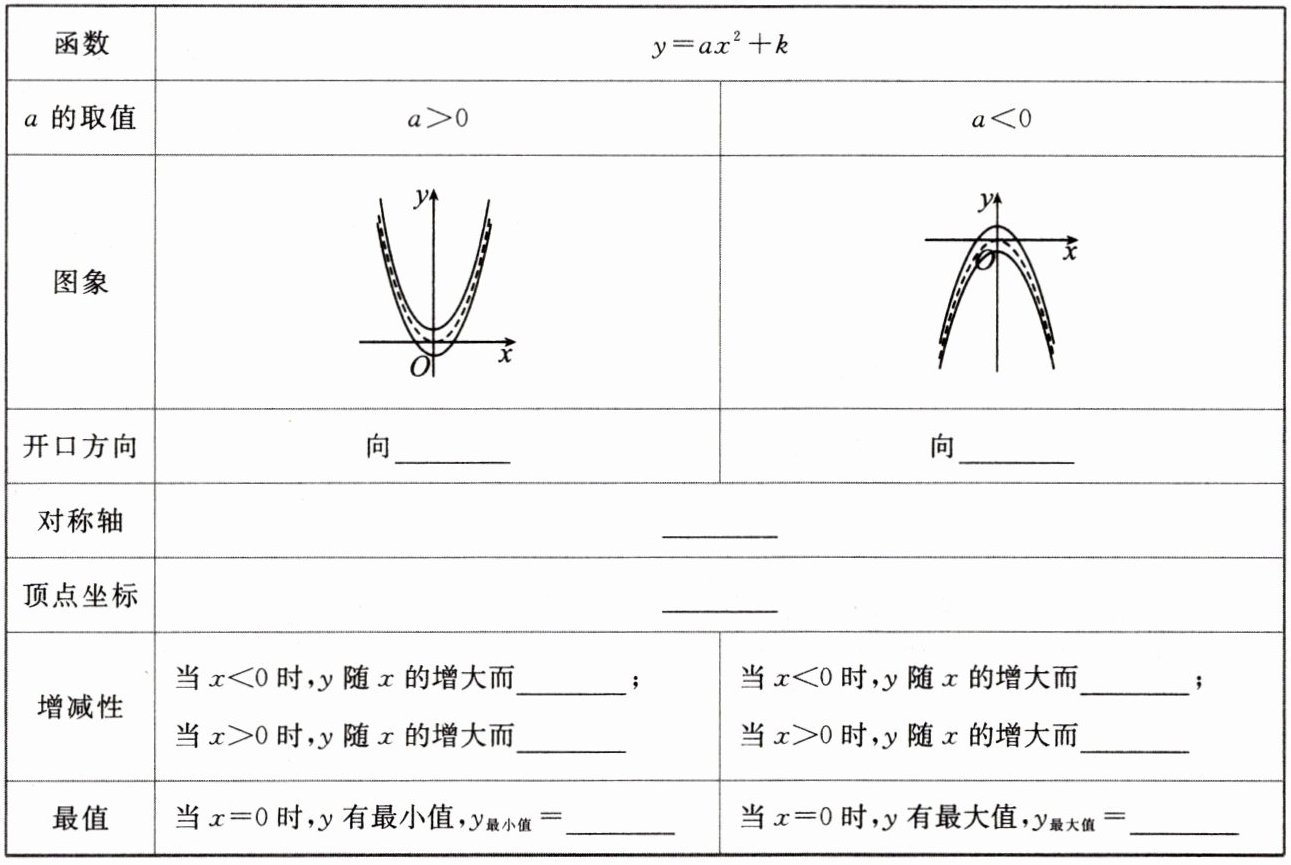
抛物线$y=ax^{2}+k$的开口方向由$a$的符号决定：当$a>0$时，开口向上；当$a<0$时，开口向下。
抛物线$y=ax^{2}+k$的对称轴是y 轴。
抛物线$y=ax^{2}+k$的顶点坐标是$(0,k)$。
当$a>0$时，在对称轴左侧（即$x<0$时），y 随 x 的增大而减小；在对称轴右侧（即$x>0$时），y 随 x 的增大而增大。
当$a<0$时，在对称轴左侧（即$x<0$时），y 随 x 的增大而增大；在对称轴右侧（即$x>0$时），y 随 x 的增大而减小。
当$a>0$时，抛物线$y=ax^{2}+k$有最低点，此时函数有最小值，最小值是k。
当$a<0$时，抛物线$y=ax^{2}+k$有最高点，此时函数有最大值，最大值是k。

答案： 上 下 y 轴 $(0,k)$ 减小 增大 增大 减小 k k

例1 (教材补充例题)(1)二次函数$y=-2x^{2}+6$的图象的对称轴是y 轴,顶点坐标是$(0,6)$,当x$＜0$时,y随x的增大而增大,当$x=$0时,y有最大值,最大值是6;

答案： 例 1
(1)y 轴 $(0,6)$ $＜0$ 0 6 

(2)若点$A(x_{1},y_{1}),B(x_{2},y_{2})$都在抛物线$y=-x^{2}+3$上,且$x_{1}＜x_{2}＜0$,则$y_{1}$____$y_{2}$(填“＞”“=”或“＜”).

答案：
(2)$＜$

变式1 若点$A(-3,y_{1}),B(-1,y_{2}),C(2,y_{3})$都在抛物线$y=\frac {2}{3}x^{2}-1$上,则$y_{1},y_{2},y_{3}$的大小关系是( )
A.$y_{1}＜y_{2}＜y_{3}$
B.$y_{3}＜y_{2}＜y_{1}$
C.$y_{1}＜y_{3}＜y_{2}$
D.$y_{2}＜y_{3}＜y_{1}$

答案： 变式 1 D

变式2 当$-2≤x≤3$时,二次函数$y=x^{2}+1$的最大值是____,最小值是____.

答案： 变式 2 10 1