第75页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
操作尝试
(1)作一个圆需要确定哪几个关键要素?
(1)作一个圆需要确定哪几个关键要素?
答案:
[操作尝试]
解:
(1)作一个圆需要确定圆心的位置和半径的大小两个关键要素.
解:
(1)作一个圆需要确定圆心的位置和半径的大小两个关键要素.
(2)经过一个已知点A作圆,你能作出多少个?
答案:
(2)能作出无数个圆.
(2)能作出无数个圆.
(3)如图24-2-3,经过两个已知点A,B作圆,你能作出多少个?圆心分布有什么特点?

答案:
(3)能作出无数个圆.圆心都在线段 的垂直平分线上,如图所示.
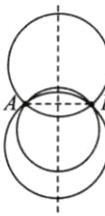
(3)能作出无数个圆.圆心都在线段 的垂直平分线上,如图所示.

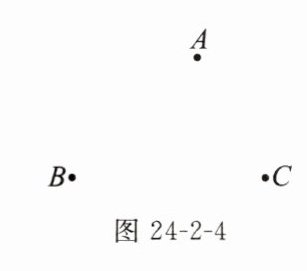
(4)如图24-2-4,经过不在同一条直线上的三个点A,B,C能不能作圆?如果能,如何确定所作圆的圆心?

答案:
(4)能.因为所求的圆要经过 A,B,C 三点,所以圆心到这三点的距离要相等,因此,圆心既要在线段 AB 的垂直平分线上,又要在线段 BC 的垂直平分线上.作法如下:
①连接 AB,BC;
②分别作出线段 AB,BC 的垂直平分线 l1 和 l2,它们交于点 O;
③以点 O 为圆心, OA (或 OB,OC) 为半径作圆,可作出经过 A,B,C 三点的圆(如图).

(4)能.因为所求的圆要经过 A,B,C 三点,所以圆心到这三点的距离要相等,因此,圆心既要在线段 AB 的垂直平分线上,又要在线段 BC 的垂直平分线上.作法如下:
①连接 AB,BC;
②分别作出线段 AB,BC 的垂直平分线 l1 和 l2,它们交于点 O;
③以点 O 为圆心, OA (或 OB,OC) 为半径作圆,可作出经过 A,B,C 三点的圆(如图).

1. 确定圆的条件:
2. 三角形的外接圆与外心:经过三角形的三个
不在同一条直线上
的三个点确定一个圆。2. 三角形的外接圆与外心:经过三角形的三个
顶点
可以作一个圆,这个圆叫做三角形的外接圆,外接圆的圆心是三角形三条边的垂直平分线
的交点,叫做这个三角形的外心。
答案:
[概括新知]1.不在同一条直线上
2.顶点 垂直平分线
2.顶点 垂直平分线
例2(教材补充例题)图24-2-5是一块残破的轮片,试作出它所在圆的圆心和半径。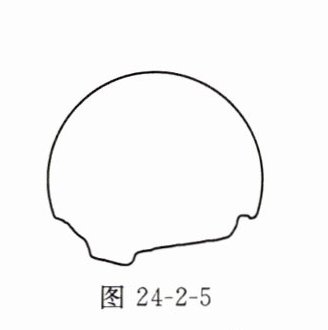

答案:
解:
1. 在残破轮片的弧上任取三点$A$、$B$、$C$。
2. 连接$AB$和$BC$。
3. 分别作$AB$和$BC$的垂直平分线,设它们相交于点$O$。
根据垂直平分线的性质:线段垂直平分线上的点到线段两端的距离相等。
因为$OA = OB$,$OB=OC$,所以$OA = OB = OC$。
所以点$O$就是该圆的圆心。
4. 连接$OA$(或$OB$、$OC$),$OA$的长度就是该圆的半径。
综上,通过上述步骤可作出残破轮片所在圆的圆心$O$和半径$OA$(或$OB$、$OC$)。
1. 在残破轮片的弧上任取三点$A$、$B$、$C$。
2. 连接$AB$和$BC$。
3. 分别作$AB$和$BC$的垂直平分线,设它们相交于点$O$。
根据垂直平分线的性质:线段垂直平分线上的点到线段两端的距离相等。
因为$OA = OB$,$OB=OC$,所以$OA = OB = OC$。
所以点$O$就是该圆的圆心。
4. 连接$OA$(或$OB$、$OC$),$OA$的长度就是该圆的半径。
综上,通过上述步骤可作出残破轮片所在圆的圆心$O$和半径$OA$(或$OB$、$OC$)。
变式 已知在Rt△ABC中,∠ACB=90°,AC=12cm,BC=5cm,求△ABC的外接圆半径。
答案:
变式 $ 6.5 \mathrm{cm} $
记方法
确定三角形外心的方法
作三角形两条边的__________,两条__________的交点为三角形的外心。
确定三角形外心的方法
作三角形两条边的__________,两条__________的交点为三角形的外心。
答案:
[记方法]垂直平分线 垂直平分线
记结论
三角形外心的位置
锐角三角形的外心在三角形的__________部,直角三角形的外心是__________,钝角三角形的外心在三角形的__________部。
三角形外心的位置
锐角三角形的外心在三角形的__________部,直角三角形的外心是__________,钝角三角形的外心在三角形的__________部。
答案:
[记结论]内 斜边的中点 外
查看更多完整答案,请扫码查看


