《2025年全品学练考九年级数学上册人教版》

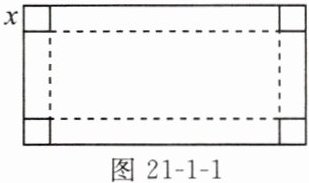
(1)如图21-1-1，有一块矩形铁皮，长100cm，宽50cm，在它的四角各切去一个同样的正方形，然后将四周突出部分折起，就能制作一个无盖方盒。如果要制作的无盖方盒的底面积为3600cm²，那么铁皮各角应切去多大的正方形？(100 - 2x)(50 - 2x) = 3600(设切去的正方形的边长为xcm，要求只列出方程，不必化简)。
(2)要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场。根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，比赛组织者应邀请多少个队参赛？$\frac{1}{2}x(x - 1) = 28$(设应邀请x个队参赛，要求只列出方程，不必化简)。
引发思考
将上述情境中列出的方程化简，并按所含未知数的降幂排列，等号右边变为0，得到两个方程x²−75x+350=0①；x²−x−56=0②。
(1)方程①②与一元一次方程的区别在哪里？
(2)方程①和②有什么共同特点呢？
(3)二次项及其系数、一次项及其系数、常数项分别是多少？

(1)未知数的最高次数是 2.
(2)①都是整式方程;②都只含有一个未知数;③未知数的最高次数都是 2.
(3)方程①的二次项是$x^{2}$，二次项系数是 1，一次项是$-75x$，一次项系数是-75，常数项是 350；
方程②的二次项是$x^{2}$，二次项系数是 1，一次项是$-x$，一次项系数是-1，常数项是-56.

答案：
(1)$(100 - 2x)(50 - 2x) = 3600$
(2)$\frac{1}{2}x(x - 1) = 28$
解:
(1)未知数的最高次数是 2.
(2)①都是整式方程;②都只含有一个未知数;③未知数的最高次数都是 2.
(3)方程①的二次项是$x^{2}$，二次项系数是 1，一次项是$-75x$，一次项系数是-75，常数项是 350；
方程②的二次项是$x^{2}$，二次项系数是 1，一次项是$-x$，一次项系数是-1，常数项是-56.

1. 一元二次方程：等号两边都是整式，只含有一个未知数(一元)，并且未知数的最高次数是2(二次)的方程，叫做一元二次方程。

答案： 整式 一 2

2. 一元二次方程的一般形式：一元二次方程的一般形式是$ax^{2}+bx+c = 0(a≠0)$，二次项、一次项、常数项分别是$ax^{2},bx,c$，二次项系数、一次项系数分别是$a,b$。

答案： $ax^{2}+bx+c = 0(a≠0)$ $ax^{2},bx,c$ $a,b$

例1(教材补充例题)下列各式是一元二次方程的是 (D)
A. x+$\frac{1}{x}$=1
B. x²+3=(x−1)²
C. ax²+bx+c=0
D. x²−1=0

答案： D

记关键
判定一元二次方程的关键要素
方程中：
(1)等号两边都是整式；
(2)只含有一个未知数；
(3)未知数的最高次数是2。

答案：
(1)整式
(2)只含有一个
(3)2