第50页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
例4 (2024贵州)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量$y$(盒)与销售单价$x$(元)是一次函数关系,下表是$y$与$x$的几组对应值.
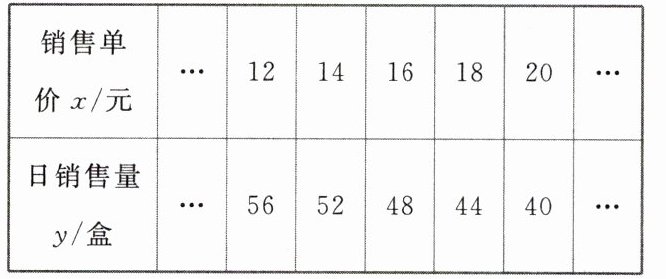
(1)求$y$与$x$之间的函数解析式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为$m$元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求$m$的值.

(1)求$y$与$x$之间的函数解析式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为$m$元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求$m$的值.
答案:
(1)$ y = - 2 x + 80 ( 10 \leq x \leq 40 ) $
(2)糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元
(3)2
(1)$ y = - 2 x + 80 ( 10 \leq x \leq 40 ) $
(2)糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元
(3)2
例5 (2024达州)如图22-T-2①,抛物线$y=ax^{2}+bx-3$与$x$轴交于点$A(-3,0)$和点$B(1,0)$,与$y$轴交于点$C$,$D$是抛物线的顶点.
(1)求抛物线的解析式.
(2)如图②,连接$AC$,$DC$,直线$AC$交抛物线的对称轴于点$M$,若$P$是直线$AC$上方抛物线上一点,且$S_{\triangle PMC}=2S_{\triangle DMC}$,求点$P$的坐标.
(3)若$N$是抛物线的对称轴上位于点$D$上方的一个动点,是否存在以点$N$,$A$,$C$为顶点的三角形是等腰三角形?若存在,请直接写出满足条件的点$N$的坐标;若不存在,请说明理由.
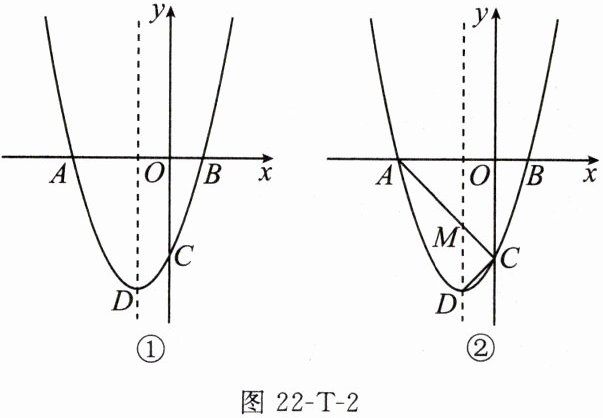
(1)求抛物线的解析式.
(2)如图②,连接$AC$,$DC$,直线$AC$交抛物线的对称轴于点$M$,若$P$是直线$AC$上方抛物线上一点,且$S_{\triangle PMC}=2S_{\triangle DMC}$,求点$P$的坐标.
(3)若$N$是抛物线的对称轴上位于点$D$上方的一个动点,是否存在以点$N$,$A$,$C$为顶点的三角形是等腰三角形?若存在,请直接写出满足条件的点$N$的坐标;若不存在,请说明理由.

答案:
解:
(1)将$ A ( - 3,0 ) $,$ B ( 1,0 ) $代入$ y = a x ^ { 2 } + b x - 3 $,得$ \left\{ \begin{array} { l } { 9 a - 3 b - 3 = 0 , } \\ { a + b - 3 = 0 , } \end{array} \right. $ 解得$ \left\{ \begin{array} { l } { a = 1 , } \\ { b = 2 , } \end{array} \right. $ 则抛物线的解析式为$ y = x ^ { 2 } + 2 x - 3 $.
(2)$ \because y = x ^ { 2 } + 2 x - 3 = x ^ { 2 } + 2 x + 1 - 4 = ( x + 1 ) ^ { 2 } - 4 $, $ \therefore D ( - 1 , - 4 ) $,抛物线的对称轴为直线$ x = - 1 $. 在$ y = x ^ { 2 } + 2 x - 3 $中,令$ x = 0 $,则$ y = - 3 $, $ \therefore C ( 0 , - 3 ) $. 过点$ D $作直线$ DG // AC $交$ y $轴于点$ G $,在点$ C $上方取点$ L $,使$ C L = 2 C G $,过点$ L $作直线$ L P // A C $交抛物线于点$ P $,如图,则点$ P $即为所求的点. 由$ A ( - 3,0 ) $,$ C ( 0 , - 3 ) $,易得直线$ AC $的解析式为$ y = - x - 3 $. $ \because D G // A C $,$ D ( - 1 , - 4 ) $, $ \therefore $直线$ DG $的解析式为$ y = - x - 5 $. 在$ y = - x - 5 $中,令$ x = 0 $,则$ y = - 5 $,$ \therefore G ( 0 , - 5 ) $,$ \therefore C G = 5 - 3 = 2 $,$ \therefore C L = 2 C G = 4 $, 则$ L ( 0,1 ) $, $ \therefore $直线$ L P $的解析式为$ y = - x + 1 $. 联立上式和抛物线的解析式,得$ x ^ { 2 } + 2 x - 3 = - x + 1 $,解得$ x _ { 1 } = 1 $,$ x _ { 2 } = - 4 $. 当$ x = 1 $时,$ y = 0 $; 当$ x = - 4 $时,$ y = 5 $, $ \therefore $点$ P $的坐标为$ ( 1,0 ) $或$ ( - 4,5 ) $.
由$ A ( - 3,0 ) $,$ C ( 0 , - 3 ) $,易得直线$ AC $的解析式为$ y = - x - 3 $. $ \because D G // A C $,$ D ( - 1 , - 4 ) $, $ \therefore $直线$ DG $的解析式为$ y = - x - 5 $. 在$ y = - x - 5 $中,令$ x = 0 $,则$ y = - 5 $,$ \therefore G ( 0 , - 5 ) $,$ \therefore C G = 5 - 3 = 2 $,$ \therefore C L = 2 C G = 4 $, 则$ L ( 0,1 ) $, $ \therefore $直线$ L P $的解析式为$ y = - x + 1 $. 联立上式和抛物线的解析式,得$ x ^ { 2 } + 2 x - 3 = - x + 1 $,解得$ x _ { 1 } = 1 $,$ x _ { 2 } = - 4 $. 当$ x = 1 $时,$ y = 0 $; 当$ x = - 4 $时,$ y = 5 $, $ \therefore $点$ P $的坐标为$ ( 1,0 ) $或$ ( - 4,5 ) $.
(3)存在以点$ N $,$ A $,$ C $为顶点的三角形是等腰三角形,点$ N $的坐标为$ ( - 1 , \pm \sqrt { 14 } ) $或$ ( - 1 , - 3 + \sqrt { 17 } ) $或$ ( - 1 , - 1 ) $.
解:
(1)将$ A ( - 3,0 ) $,$ B ( 1,0 ) $代入$ y = a x ^ { 2 } + b x - 3 $,得$ \left\{ \begin{array} { l } { 9 a - 3 b - 3 = 0 , } \\ { a + b - 3 = 0 , } \end{array} \right. $ 解得$ \left\{ \begin{array} { l } { a = 1 , } \\ { b = 2 , } \end{array} \right. $ 则抛物线的解析式为$ y = x ^ { 2 } + 2 x - 3 $.
(2)$ \because y = x ^ { 2 } + 2 x - 3 = x ^ { 2 } + 2 x + 1 - 4 = ( x + 1 ) ^ { 2 } - 4 $, $ \therefore D ( - 1 , - 4 ) $,抛物线的对称轴为直线$ x = - 1 $. 在$ y = x ^ { 2 } + 2 x - 3 $中,令$ x = 0 $,则$ y = - 3 $, $ \therefore C ( 0 , - 3 ) $. 过点$ D $作直线$ DG // AC $交$ y $轴于点$ G $,在点$ C $上方取点$ L $,使$ C L = 2 C G $,过点$ L $作直线$ L P // A C $交抛物线于点$ P $,如图,则点$ P $即为所求的点.
 由$ A ( - 3,0 ) $,$ C ( 0 , - 3 ) $,易得直线$ AC $的解析式为$ y = - x - 3 $. $ \because D G // A C $,$ D ( - 1 , - 4 ) $, $ \therefore $直线$ DG $的解析式为$ y = - x - 5 $. 在$ y = - x - 5 $中,令$ x = 0 $,则$ y = - 5 $,$ \therefore G ( 0 , - 5 ) $,$ \therefore C G = 5 - 3 = 2 $,$ \therefore C L = 2 C G = 4 $, 则$ L ( 0,1 ) $, $ \therefore $直线$ L P $的解析式为$ y = - x + 1 $. 联立上式和抛物线的解析式,得$ x ^ { 2 } + 2 x - 3 = - x + 1 $,解得$ x _ { 1 } = 1 $,$ x _ { 2 } = - 4 $. 当$ x = 1 $时,$ y = 0 $; 当$ x = - 4 $时,$ y = 5 $, $ \therefore $点$ P $的坐标为$ ( 1,0 ) $或$ ( - 4,5 ) $.
由$ A ( - 3,0 ) $,$ C ( 0 , - 3 ) $,易得直线$ AC $的解析式为$ y = - x - 3 $. $ \because D G // A C $,$ D ( - 1 , - 4 ) $, $ \therefore $直线$ DG $的解析式为$ y = - x - 5 $. 在$ y = - x - 5 $中,令$ x = 0 $,则$ y = - 5 $,$ \therefore G ( 0 , - 5 ) $,$ \therefore C G = 5 - 3 = 2 $,$ \therefore C L = 2 C G = 4 $, 则$ L ( 0,1 ) $, $ \therefore $直线$ L P $的解析式为$ y = - x + 1 $. 联立上式和抛物线的解析式,得$ x ^ { 2 } + 2 x - 3 = - x + 1 $,解得$ x _ { 1 } = 1 $,$ x _ { 2 } = - 4 $. 当$ x = 1 $时,$ y = 0 $; 当$ x = - 4 $时,$ y = 5 $, $ \therefore $点$ P $的坐标为$ ( 1,0 ) $或$ ( - 4,5 ) $. (3)存在以点$ N $,$ A $,$ C $为顶点的三角形是等腰三角形,点$ N $的坐标为$ ( - 1 , \pm \sqrt { 14 } ) $或$ ( - 1 , - 3 + \sqrt { 17 } ) $或$ ( - 1 , - 1 ) $.
查看更多完整答案,请扫码查看


