《2025年全品学练考九年级数学上册人教版》

如图21-3-2，要设计一本书的封面，封面长27cm，宽21cm，正中央是一个与整个封面长宽比例相同的矩形。如果要使四周的边衬所占面积是封面面积的四分之一，上、下边衬等宽，左、右边衬等宽，应如何设计四周边衬的宽度（结果保留小数点后一位）？
引发思考
（1）根据题目的已知条件，得中央的矩形的长宽之比是27:21=9:7，那你知道上、下边衬与左、右边衬的宽度之比是多少吗？请你算一算。
（2）根据上、下边衬与左、右边衬的宽度之比，如何设未知数、列方程？
（3）解方程时教材上先把方程整理成了一般形式，再用公式法求解，你有更简便的解法吗？
（4）方程的哪个根符合实际意义？为什么？
（5）如果换一种设未知数的方法，是否可以更简单地解决上面的问题？请你试一试。

答案： （1）求上、下边衬与左、右边衬的宽度之比
设上、下边衬的宽均为$9x cm$，左、右边衬的宽均为$7x cm$。
因为中央矩形与整个封面长宽比例相同，封面长$27cm$，宽$21cm$，长宽比为$9:7$，所以上、下边衬与左、右边衬的宽度之比是$9:7$。
（2）设未知数、列方程
设上、下边衬的宽均为$9x cm$，左、右边衬的宽均为$7x cm$。
封面面积为$27×21$，中央矩形面积为$(27 - 18x)(21 - 14x)$。
已知四周的边衬所占面积是封面面积的四分之一，则中央矩形面积是封面面积的$\frac{3}{4}$，可列方程$(27 - 18x)(21 - 14x)=\frac{3}{4}×27×21$。
（3）更简便的解法
$\begin{aligned}(27 - 18x)(21 - 14x)&=\frac{3}{4}×27×21\\frac{27 - 18x}{27}×\frac{21 - 14x}{21}&=\frac{3}{4}\\(1 - \frac{2}{3}x)(1 - \frac{2}{3}x)&=\frac{3}{4}\\(1 - \frac{2}{3}x)^2&=\frac{3}{4}\\1 - \frac{2}{3}x&=\pm\frac{\sqrt{3}}{2}\\frac{2}{3}x&=1\pm\frac{\sqrt{3}}{2}\\x&=\frac{3}{2}(1\pm\frac{\sqrt{3}}{2})\end{aligned}$
取$x=\frac{3}{2}(1 - \frac{\sqrt{3}}{2})\approx\frac{3}{2}(1 - 0.866)= 0.201$
（4）判断方程根的实际意义
$x_1=\frac{3}{2}(1 + \frac{\sqrt{3}}{2})$，此时$18x=18×\frac{3}{2}(1 + \frac{\sqrt{3}}{2})\gt27$，$14x=14×\frac{3}{2}(1 + \frac{\sqrt{3}}{2})\gt21$，不符合实际意义，舍去。
$x_2=\frac{3}{2}(1 - \frac{\sqrt{3}}{2})$，此时$18x = 18×\frac{3}{2}(1 - \frac{\sqrt{3}}{2})\approx 1.8$，$14x=14×\frac{3}{2}(1 - \frac{\sqrt{3}}{2})\approx 1.4$，符合实际意义。
（5）换一种设未知数的方法
设中央矩形的长为$9y cm$，宽为$7y cm$。
则$9y×7y=\frac{3}{4}×27×21$，即$y^2=\frac{3}{4}×\frac{27×21}{9×7}=\frac{27}{4}$，$y = \frac{3\sqrt{3}}{2}\approx2.6$。
上、下边衬宽：$\frac{27 - 9y}{2}=\frac{27 - 9×\frac{3\sqrt{3}}{2}}{2}\approx\frac{27 - 23.38}{2}=1.8(cm)$。
左、右边衬宽：$\frac{21 - 7y}{2}=\frac{21 - 7×\frac{3\sqrt{3}}{2}}{2}\approx\frac{21 - 18.52}{2}=1.2(cm)$。
综上，（1）上、下边衬与左、右边衬的宽度之比是$\boldsymbol{9:7}$；（2）设上、下边衬的宽均为$9x cm$，左、右边衬的宽均为$7x cm$，列方程$(27 - 18x)(21 - 14x)=\frac{3}{4}×27×21$；（3）如上述更简便解法；（4）$x=\frac{3}{2}(1 - \frac{\sqrt{3}}{2})$符合实际意义，原因如上述；（5）如上述换元法。

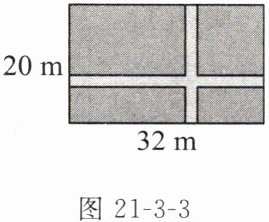
例（教材补充例题）如图21-3-3，在一块宽为20m，长为32m的矩形地面上修筑同样宽的一横一纵两条道路，余下的部分种上草坪，要使草坪的面积为540m²，道路的宽为多少米？

答案： 例 2 m