《2025年全品学练考九年级数学上册人教版》

观察猜想
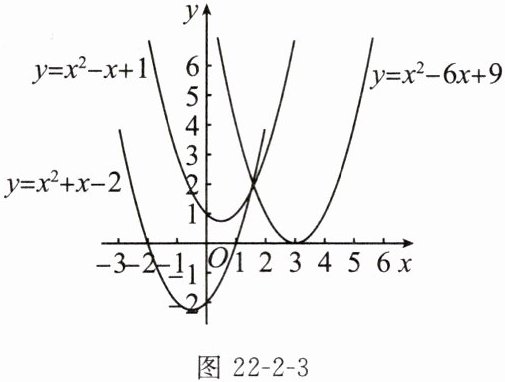
①如图22-2-3所示，下列二次函数的图象与x轴有公共点吗？②如果有，公共点的横坐标是多少？③当x取公共点的横坐标时，函数值是多少？④由此，你能得出相应的一元二次方程的根吗？⑤反过来，由一元二次方程的根的情况，可以确定相应的二次函数的图象与x轴的位置关系吗？
(1)y=x²+x-2；(2)y=x²-6x+9；(3)y=x²-x+1.

答案： ##### [观察猜想]
解:
(1)抛物线 $y = x^{2}+x - 2$ 与 x 轴有两个公共点,它们的横坐标是 -2,1.当 x 取公共点的横坐标时,函数值是 0.由此得出方程 $x^{2}+x - 2 = 0$ 的根是 -2,1.
(2)抛物线 $y = x^{2}-6x + 9$ 与 x 轴只有一个公共点,这点的横坐标是 3.当 $x = 3$ 时,函数值是 0.由此得出方程 $x^{2}-6x + 9 = 0$ 有两个相等的实数根 3.
(3)抛物线 $y = x^{2}-x + 1$ 与 x 轴没有公共点.由此可知,方程 $x^{2}-x + 1 = 0$ 没有实数根.
反过来,由一元二次方程的根的情况,也可以确定相应的二次函数的图象与 x 轴的位置关系.

抛物线与x轴的位置关系与对应的一元二次方程的根的情况之间的关系：

[概括新知] 两个不等的 两个相等的 没有

答案： ##### [概括新知] 两个不等的 两个相等的 没有

例2(教材补充例题)判断下列函数的图象与x轴的公共点情况，并说明理由.
(1)y=2x²-3x；(2)y=-x²-4x-1；(3)y=x²+2x+5.

答案： 例 2 解:
(1)函数 $y = 2x^{2}-3x$ 的图象与 x 轴有两个公共点.
理由:令 $y = 0$,则 $2x^{2}-3x = 0$.
∵$(-3)^{2}-4×2×0 = 9 ＞ 0$,
∴该方程有两个不等的实数根,故函数 $y = 2x^{2}-3x$ 的图象与 x 轴有两个公共点.
(2)函数 $y = -x^{2}-4x - 1$ 的图象与 x 轴有两个公共点.
理由:令 $y = 0$,则 $-x^{2}-4x - 1 = 0$.
∵$(-4)^{2}-4×(-1)×(-1) = 12 ＞ 0$,
∴该方程有两个不等的实数根,故函数 $y = -x^{2}-4x - 1$ 的图象与 x 轴有两个公共点.
(3)函数 $y = x^{2}+2x + 5$ 的图象与 x 轴没有公共点.
理由:令 $y = 0$,则 $x^{2}+2x + 5 = 0$.
∵$2^{2}-4×1×5 = -16 ＜ 0$,
∴该方程没有实数根,故函数 $y = x^{2}+2x + 5$ 的图象与 x 轴没有公共点.

例3(教材典题)利用函数图象求方程x²-2x-2=0的实数根(结果保留小数点后一位).

答案： 例 3 $x_{1}≈-0.7,x_{2}≈2.7$