《2025年全品学练考九年级数学上册人教版》

操作尝试
通过作图分析怎样移动抛物线$y = -\frac{1}{2}x^2$就可以得到抛物线$y = -\frac{1}{2}(x + 1)^2 - 1$，你有几种移动方法？

答案： 1. 方法一：
先根据抛物线平移规律“左加右减，上加下减”。
对于抛物线$y = -\frac{1}{2}x^{2}$，先向左平移$1$个单位：
根据“左加右减”原则，$y = -\frac{1}{2}x^{2}$变为$y = -\frac{1}{2}(x + 1)^{2}$（当$x$变为$x + 1$时，图象向左平移$1$个单位）。
再根据“上加下减”原则，将$y = -\frac{1}{2}(x + 1)^{2}$向下平移$1$个单位，得到$y=-\frac{1}{2}(x + 1)^{2}-1$。
2. 方法二：
先向下平移$1$个单位：
根据“上加下减”原则，$y = -\frac{1}{2}x^{2}$变为$y = -\frac{1}{2}x^{2}-1$。
再根据“左加右减”原则，将$y = -\frac{1}{2}x^{2}-1$向左平移$1$个单位，$x$变为$x + 1$，得到$y = -\frac{1}{2}(x + 1)^{2}-1$。
所以有两种移动方法。

例3（教材补充例题）将二次函数$y = 3x^2$的图象向右平移5个单位长度，再向上平移1个单位长度后，得到的图象的解析式为$ y = 3(x - 5)^2 + 1 $.

答案： $ y = 3(x - 5)^2 + 1 $

例4（教材典题）要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管应多长？

答案： 2.25 m

1.（2024哈尔滨）二次函数$y = 2(x + 1)^2 + 3$的最小值是（D）
A. $-1$
B. $1$
C. $2$
D. $3$

答案： D

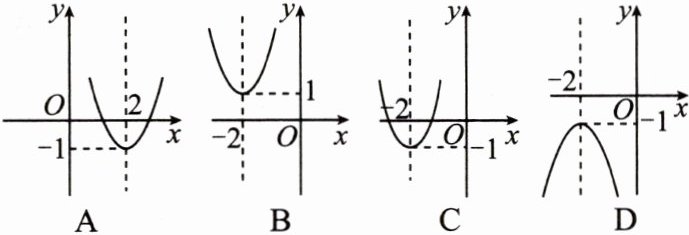
2. 二次函数$y = 2(x + 2)^2 - 1$的图象是（C）

答案： C

3.（2024滨州）将抛物线$y = -x^2$先向右平移1个单位长度，再向上平移2个单位长度，则平移后抛物线的顶点坐标为(1, 2).

答案： $ (1, 2) $

4. 把二次函数$y = a(x - h)^2 + k$的图象先向左平移2个单位长度，再向上平移4个单位长度，得到二次函数$y = \frac{1}{2}(x + 1)^2 - 1$的图象.
（1）直接写出$a$，$h$，$k$的值；
（2）指出二次函数$y = a(x - h)^2 + k$的图象的开口方向、对称轴和顶点坐标.

答案： 解：
(1) $ a = \frac{1}{2} $，$ h = 1 $，$ k = -5 $。
(2) 二次函数 $ y = a(x - h)^2 + k $ 的图象开口向上，对称轴是直线 $ x = 1 $，顶点坐标是 $ (1, -5) $。