第65页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
观察思考
如图24-1-1,观察画圆的过程,你能说出圆是如何画出来的吗?
如图24-1-1,观察画圆的过程,你能说出圆是如何画出来的吗?

解:在一个平面内,线段$OA$绕它固定的一个端点$O$旋转一周,另一个端点$A$所形成的图形叫做圆。固定的端点$O$叫做圆心,线段$OA$叫做半径。 所以圆是通过将线段的一端固定,另一端绕固定端旋转一周画出来的。
答案:
解:在一个平面内,线段$OA$绕它固定的一个端点$O$旋转一周,另一个端点$A$所形成的图形叫做圆。固定的端点$O$叫做圆心,线段$OA$叫做半径。 所以圆是通过将线段的一端固定,另一端绕固定端旋转一周画出来的。
认识概念
圆的定义:
(1)如图24-1-2,在一个平面内,线段______绕它固定的一个______旋转一周,另一个端点A所形成的图形叫做圆。其固定的端点O叫做______,线段OA叫做______。以点O为圆心的圆,记作$\odot O$,读作“圆O”。
(2)圆心为O、半径为r的圆可以看成是所有到定点O的______等于______的点的集合。

圆的定义:
(1)如图24-1-2,在一个平面内,线段______绕它固定的一个______旋转一周,另一个端点A所形成的图形叫做圆。其固定的端点O叫做______,线段OA叫做______。以点O为圆心的圆,记作$\odot O$,读作“圆O”。
(2)圆心为O、半径为r的圆可以看成是所有到定点O的______等于______的点的集合。

答案:
(1)OA 端点O 圆心 半径
(2)距离 定长r
(1)OA 端点O 圆心 半径
(2)距离 定长r
例1 (教材典题)矩形ABCD的对角线AC,BD相交于点O。求证:A,B,C,D四个点在以点O为圆心的同一个圆上。
答案:
例1 证明:
∵四边形ABCD为矩形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OC=OB=OD,
∴A,B,C,D四个点在以点O为圆心,OA为半径的圆上(如图)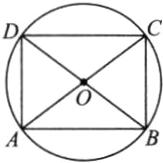
例1 证明:
∵四边形ABCD为矩形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OC=OB=OD,
∴A,B,C,D四个点在以点O为圆心,OA为半径的圆上(如图)

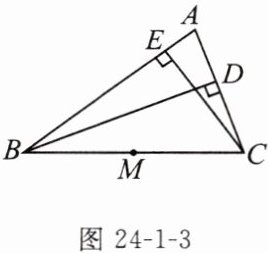
变式 已知:如图24-1-3,BD,CE是$\triangle ABC$的高,M为BC的中点。求证:点B,C,D,E在以点M为圆心的同一个圆上。

答案:
变式 证明:连接ME,MD.
∵BD,CE是△ABC的高,M为BC的中点,
∴ME=MB=MC=$\frac{1}{2}$BC,MD=MB=MC=$\frac{1}{2}$BC,
∴ME=MD=MB=MC,
∴点B,C,D,E在以点M为圆心的同一个圆上.
∵BD,CE是△ABC的高,M为BC的中点,
∴ME=MB=MC=$\frac{1}{2}$BC,MD=MB=MC=$\frac{1}{2}$BC,
∴ME=MD=MB=MC,
∴点B,C,D,E在以点M为圆心的同一个圆上.
查看更多完整答案,请扫码查看


