《2025年全品学练考九年级数学上册人教版》

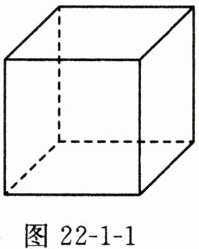
(1)如图22-1-1所示是一个正方体,如果改变正方体的棱长x,那么正方体的表面积y会随之改变,y与x之间有什么关系?
(2)n个球队参加比赛,每两队之间进行一场比赛.比赛的场次数m与球队数n有什么关系?
(3)某种产品现在的年产量是20t,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
引发思考
观察(1)~(3)中所得到的函数解析式,从含有自变量式子的最高次数上找找这些函数有什么共同特点.

答案： [问题情境]
解：
(1)y 是 x 的函数，它们的具体关系可以表示为 $ y = 6x^{2} $。
(2)m 是 n 的函数，它们的具体关系可以表示为 $ m = \frac{1}{2}n^{2} - \frac{1}{2}n $。
(3)y 是 x 的函数，它们的具体关系可以表示为 $ y = 20x^{2} + 40x + 20 $。
[引发思考]
解：函数都是用自变量的二次式表示的。

二次函数的定义:一般地,形如$ y = ax^{2} + bx + c $(a,b,c是常数,a≠0)的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.

答案： [概括新知]
$ y = ax^{2} + bx + c $ 二次项系数 一次项系数 常数项

例1(教材补充例题)下列函数中,属于二次函数的是 (C)
A.$ y = x ^ { 2 } + \frac { 1 } { x } $
B.$ y = ( x + 1 ) ^ { 2 } - x ^ { 2 } $
C.$ y = 2 x ^ { 2 } - 7 x $
D.$ y = a x ^ { 2 } + b x + c $

答案： 例 1 C 

变式若$ y = m x ^ { | m - 1 | + 1 } + 1 $是关于x的二次函数,则m的值为________.

答案： 变式 2

例2(教材补充例题)下列函数中,哪些是关于x的二次函数?哪些不是?若是二次函数,请指出其二次项系数、一次项系数以及常数项.
(1)$ y = 3 - 2 x ^ { 2 } $;
(2)$ y = ( 2 x + 1 ) ^ { 2 } - 4 x ^ { 2 } $.

答案： 例 2 解：
(1)是二次函数，二次项系数、一次项系数以及常数项分别是 -2，0，3。
(2)不是二次函数。