《2025年全品学练考九年级数学上册人教版》

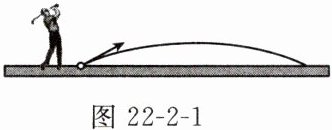
如图22-2-1，以40m/s的速度将小球沿与地面成30°角的方向击出时，小球的飞行路线将是一条抛物线.小球的飞行高度h(单位：m)与飞行时间t(单位：s)之间具有函数关系h=20t-5t².
(1)小球的飞行高度能否达到15m？如果能，需要多少飞行时间？
(2)你能结合图22-2-1指出为什么在两个时间小球的高度为15m吗？
(3)小球的飞行高度能否达到20m？如果能，需要多少飞行时间？
(4)你能结合图22-2-1指出为什么只在一个时间小球的高度为20m吗？
(5)小球的飞行高度能否达到20.5m？为什么？
(6)小球从飞出到落地要用多少时间？

答案：
(1)能 当小球飞行 1s 和 3s 时,它的飞行高度为 15m
(2)
∵小球在某一时间达到 15m,然后继续上升,达到最大高度后开始下落,经过一段时间,小球的高度又回落到 15m,
∴在两个时间小球的高度为 15m.
(3)能 当小球飞行 2s 时,它的飞行高度为 20m
(4)
∵小球在某一时间达到最大高度 20m,
∴只在一个时间小球的高度为 20m.
(5)不能.理由:解方程 $20.5 = 20t - 5t^{2}$,$t^{2}-4t + 4.1 = 0$.
∵$(-4)^{2}-4×4.1 ＜ 0$,
∴方程无实数根.这就是说,小球的飞行高度达不到 20.5m.
(6)4s

概括归纳
二次函数与一元二次方程的关系：如果抛物线y=ax²+bx+c与x轴有公共点，那么公共点的横坐标就是一元二次方程ax²+bx+c=0的根.

答案：   横坐标

例1(教材补充例题)如图22-2-2，二次函数y=ax²+bx+c的部分图象与x轴的一个公共点坐标为(-1,0)，则关于x的方程ax²+bx+c=0的根为(C)

A.x=-1
B.x=3
C.x₁=-1，x₂=3
D.x₁=-1，x₂=1

答案： 例 1 C